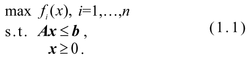| Gwo-Hshiung Tzeng New Concepts and Trends of Hybrid MCDM for Tomorrow |
|
-
Theories
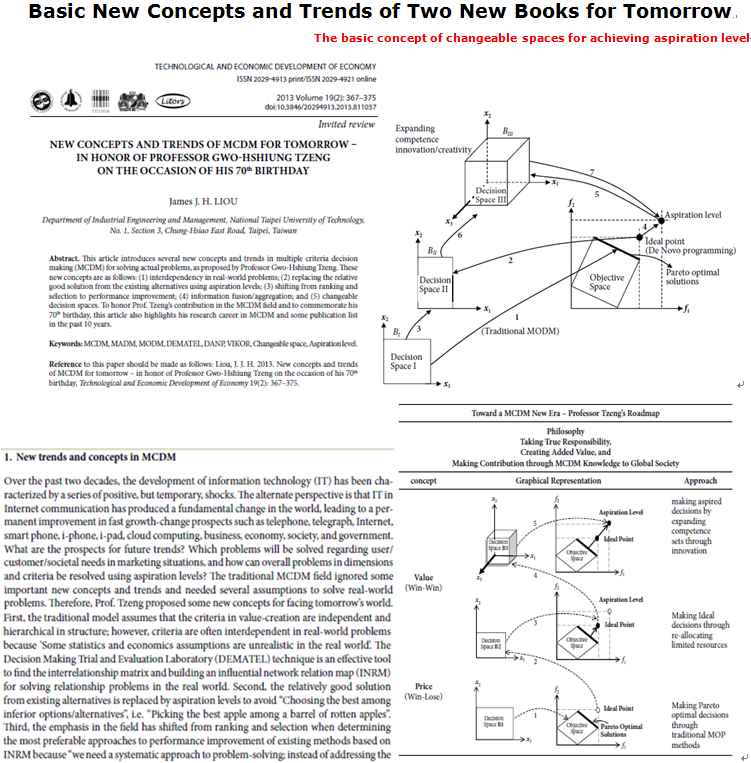
- New concepts and trends of MCDM for tomorrow - in honor of Professor Gwo-Hshiung Tzeng on the occasion of his 70th birthday
- COMMENTS ON “MULTIPLE CRITERIA DECISION MAKING (MCDM) METHODS IN ECONOMICS: AN OVERVIEW”
- New thinking of multi-objective programming with changeable space – in search of excellence
- A Hybrid Dynamic MADM Model for Problem-Improvement in Economics and Business
- A Fuzzy Integral-based Model for Supplier Evaluation and Improvement
- New Combined Hybrid Approaches
- DEMATEL and DANP
- Vitae
- News !
- Publications
- Lectures
-
MCDM
- Websites >
-
Fuzzy (IJFS)
>
- FMCDM with Fuzzy DEMATEL Approach for Customers' Choice Behavior Model
- A Novel Method for Fuzzy Measure Identification
- Combining Hybrid MADM with Fuzzy Integral for Exploring the Smart Phone Improvement in M-Generation
- Environmental Strategic Orientations for Improving Green Innovation Performance in Fuzzy Environment - Using New Fuzzy Hybrid MCDM Model
- DRSA-Based Neuro-Fuzzy Inference Systems for the Financial Performance Prediction of Commercial Banks
- New Books
- Contact
New Books, Gwo-Hshiung Tzeng
Briefing of the New Book
Fig. 1.1 New hybrid approach in MCDM based on three pillars
Fig. 2.2 Main ideas of problem-solving in new hybrid MCDM
Fig. 2.3 Conceptual framework of new hybrid/combined MCDM
Chapter 1 INTRODUCTION
Chapter 2 NEW CONCEPTS AND TRENDS IN MCDM
PART ONE
Chapter 3 BASIC CONCEPTS OF DEMATEL AND ITS REVISION
Chapter 4 DEMATEL TECHNIQUE FOR FORMING INRM AND DANP WEIGHTS
Chapter 5 TRADITIONAL MADM AND NEW HYBRID MADM FOR PROBLEM-SOLVING
Chapter 6 MODM WITH DE NOVO AND CHANGEABLE SPACES
Chapter 7 MULTIPLE RULES-BASED DECISION-MAKING FOR SOLVING DATA-CENTRIC PROBLEMS
PART TWO
Chapter 8 THE CASE OF DEMATEL FOR ASSESSING INFORMATION RISK
Chapter 9 E-STORE BUSINESS EVALUATION AND IMPROVEMENT USING A HYBRID MADM MODEL
Chapter 10 IMPROVING THE PERFORMANCE OF GREEN SUPPLIERS IN THE TFT-LCD INDUSTRY
Chapter 11 EXPLORING SMARTPHONE IMPROVEMENTS BASED ON A HYBRID MADM MODEL
Chapter 12 EVALUATING THE DEVELOPMENT OF BUSINESS-TO-BUSINESS M-COMMERCE OF SMES
Chapter 13 EVALUATION AND SELECTION OF GLAMOUR STOCKS BY A HYBRID MADM MODEL
Chapter 14 NON-ADDITIVE HYBRID MADM MODEL FOR SELECTING AND IMPROVING SUPPLIERS
Chapter 15 NEW PERSPECTIVE OF MODELING STRATEGIC ALLIANCES BY DE NOVO PROGRAMMING
Chapter 16 AUTOMATED FACTORY PLANNING USING THE NEW IDEA OF CHANGEABLE SPACES
Chapter 17 FUZZY INFERENCE SUPPORTED MRDM FOR TECHNICAL ANALYSIS: A CASE OF STOCK INVESTMENT
Chapter 18 FINANCIAL IMPROVEMENTS OF COMMERCIAL BANKS USING A HYBRID MRDM APPROACH
Chapter 19 FCA-BASED DANP MODEL USING THE ROUGH SET APPROACH: A CASE OF SEMICONDUCTOR COMPANIES
Chapter 20 HYBRID BIPOLAR MRDM MODEL FOR BUSINESS ANALYTICS
Chapter 2 NEW CONCEPTS AND TRENDS IN MCDM
PART ONE
Chapter 3 BASIC CONCEPTS OF DEMATEL AND ITS REVISION
Chapter 4 DEMATEL TECHNIQUE FOR FORMING INRM AND DANP WEIGHTS
Chapter 5 TRADITIONAL MADM AND NEW HYBRID MADM FOR PROBLEM-SOLVING
Chapter 6 MODM WITH DE NOVO AND CHANGEABLE SPACES
Chapter 7 MULTIPLE RULES-BASED DECISION-MAKING FOR SOLVING DATA-CENTRIC PROBLEMS
PART TWO
Chapter 8 THE CASE OF DEMATEL FOR ASSESSING INFORMATION RISK
Chapter 9 E-STORE BUSINESS EVALUATION AND IMPROVEMENT USING A HYBRID MADM MODEL
Chapter 10 IMPROVING THE PERFORMANCE OF GREEN SUPPLIERS IN THE TFT-LCD INDUSTRY
Chapter 11 EXPLORING SMARTPHONE IMPROVEMENTS BASED ON A HYBRID MADM MODEL
Chapter 12 EVALUATING THE DEVELOPMENT OF BUSINESS-TO-BUSINESS M-COMMERCE OF SMES
Chapter 13 EVALUATION AND SELECTION OF GLAMOUR STOCKS BY A HYBRID MADM MODEL
Chapter 14 NON-ADDITIVE HYBRID MADM MODEL FOR SELECTING AND IMPROVING SUPPLIERS
Chapter 15 NEW PERSPECTIVE OF MODELING STRATEGIC ALLIANCES BY DE NOVO PROGRAMMING
Chapter 16 AUTOMATED FACTORY PLANNING USING THE NEW IDEA OF CHANGEABLE SPACES
Chapter 17 FUZZY INFERENCE SUPPORTED MRDM FOR TECHNICAL ANALYSIS: A CASE OF STOCK INVESTMENT
Chapter 18 FINANCIAL IMPROVEMENTS OF COMMERCIAL BANKS USING A HYBRID MRDM APPROACH
Chapter 19 FCA-BASED DANP MODEL USING THE ROUGH SET APPROACH: A CASE OF SEMICONDUCTOR COMPANIES
Chapter 20 HYBRID BIPOLAR MRDM MODEL FOR BUSINESS ANALYTICS
Please visit the website of CRC Press (Taylor & Francis Group) for more information about this upcoming new book:
https://www.crcpress.com/New-Concepts-and-Trends-of-Hybrid-Multiple-Criteria-Decision-Making/Tzeng-Shen/p/book/9781498777087
https://www.crcpress.com/New-Concepts-and-Trends-of-Hybrid-Multiple-Criteria-Decision-Making/Tzeng-Shen/p/book/9781498777087
Preview of the new book
CHAPTER 1
INTRODUCTION
CHAPTER 1
INTRODUCTION
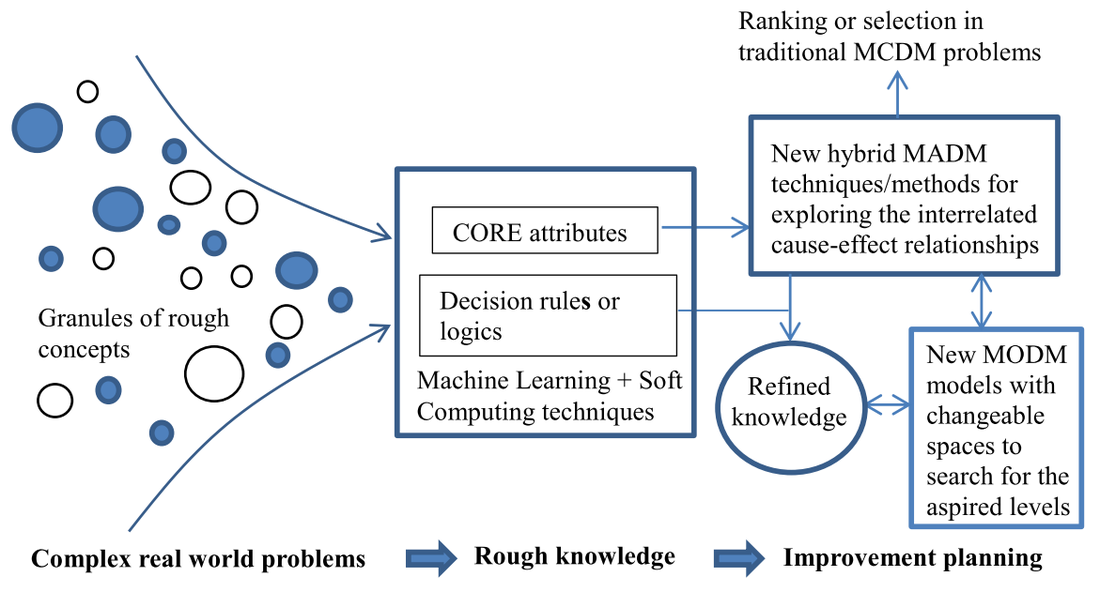
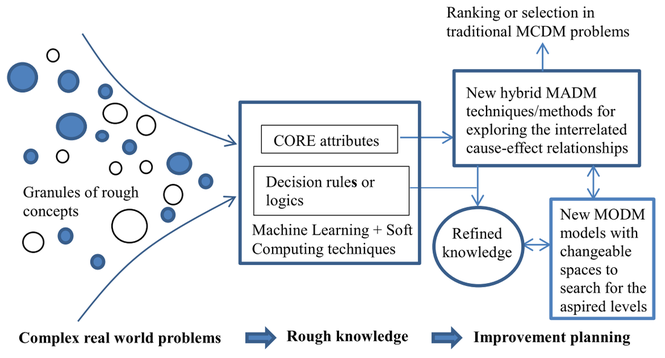
This book introduces new hybrid multiple criteria decision-making (MCDM) methods for solving real-world problems with improvement planning. Traditional MCDM ignores some vital issues such as certain unrealistic assumptions and constraints. This book proposes several new concepts and demonstrates how current trends in hybrid MCDM models can facilitate solving practical problems (Liou and Tzeng 2012; Liou 2013; Peng and Tzeng 2013; Huang and Tzeng 2014). In this book, several new techniques are introduced, including the dominance-based rough set approach (DRSA), the decision-rule-based bipolar method, formal concept analysis, the DEMATEL technique for building influential network relation maps and finding the influential weights of a DEMATEL-based analytic network process (ANP), modified evaluation methods (e.g., SAW, VIKOR, Grey analysis, PROMETHEE, and ELECTRE) for setting performance improvement strategies, and multiple objective programming (MOP) with changeable spaces for optimizing (aspiration-level) resource allocation (Fig 1.1).
Hybrid MCDM models have already successfully analyzed the characteristics of various real-world problems (Zavadskas and Turskis 2011; Huang and Tzeng 2011; Liou and Tzeng 2012; Peng and Tzeng 2013; Greco et al. 2016). Several empirical cases from the financial and information technology (IT) industries can illustrate MCDM methods for researchers and practitioners, and are provided in PART TWO.
1.1 Overview of Traditional MCDM Techniques and Methods
The goals of traditional decision-making can be sorted into several categories: ranking, selection, and optimization. A typical MCDM problem usually begins with identifying the goal and the related criteria, attributes, or constraints. Subsequently, to evaluate the available alternative solutions to a problem, researchers must collect the preferences of the decision makers (DMs) regarding the available alternatives in the context of the pertinent criteria. If only a single criterion (or attribute) were considered, it would be intuitive to choose the alternative with the highest preference rating. In the presence of multiple criteria (or attributes), DMs are usually compelled to compromise among a group of alternatives even though none of the alternatives outperforms or dominates the others on all the criteria. Therefore, various quantitative methods have been proposed to support DMs who must make decisions that advance predefined goals.
Following Hwang and Yoon (1981), MCDM problems can be further categorized into two subfields: multiple attribute decision-making (MADM) and multiple objective decision-making (MODM); MADM is concerned with ranking or selecting by evaluating predetermined alternatives, and MODM is aimed at identifying the optimal outcome by searching for an efficient frontier within a solution space under the given constraints. Most conventional MCDM research comprises these two subfields of MADM and MODM (Köksalan et al. 2011).
Because MADM focuses on evaluating alternatives according to a DM’s preference, it is reasonable to adopt the utility theory from economics to depict a DM’s preferences for multiple attributes in the form of preference (value or utility) functions; this is performed in multiple attribute utility theory (MAUT). Although MAUT has solid foundations from economic theories, its essential assumption is based on the independence of attributes, which is not realistic in most real-world cases. The utility additive (UTA) method extends the MAUT method and uses regression and linear programming techniques to reach the solution of optimal value (utility) that is consistent with a DM’s global preferences. However, just as MAUT assumes the independence of attributes, UTA methods assume the independence of variables (i.e., attributes or criteria).
Another prevalent approach in MADM research is the analytic hierarchy process (AHP), which was introduced by Saaty (1972, 1992). AHP decomposes a problem into hierarchical levels (mainly dealing with two levels: dimensions and criteria), and uses pairwise comparisons to calculate a DM’s global preferences regarding the final goal. Certain aggregation methods (additive type operators), such as SAW, TOPSIS, VIKOR, and PROMETHEE, may integrate with the preference weights obtained by traditional MADM methods in order to support DMs who must make the final ranking or selection. MADM methods are mainly devised for evaluations.
By contrast, MODM is more suitable for designing or planning by optimizing the allocation of limited resources. Because real-world environments are often full of competing and even conflicting constraints, DMs may rely on MODM methods to achieve multiple goals simultaneously; mathematical programming is mainly adopted to solve those optimization problems. Nevertheless, traditional MODM optimization methods are only concerned with Pareto optimal solutions (also called non-inferior non-dominated solutions or effective solutions) within a system; notions of essential optimization are not addressed (Zeleny 1990). When encountering an MODM problem, DMs usually find that optimization of all objectives in a given system is impossible. Most problems involve tradeoffs; one cannot increase the levels of satisfaction for one objective without reducing those for another. Conventional multiobjective programming techniques are often applied to search for non-inferior solutions (i.e., Pareto optimal solutions) or compromise solutions, which are transformed into single-objective programs that produce solutions acceptable to DMs. When objective functions conflict with one another, DMs can formalize tradeoffs by using conventional methods.
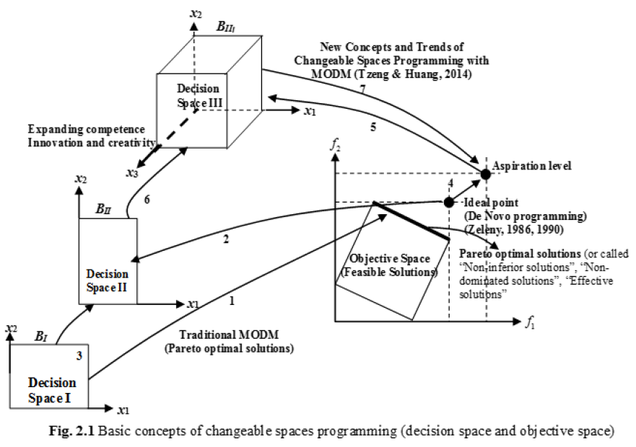
Because tradeoffs often prevent the simultaneous optimization of all criteria, Zeleny (1982) offered an MODM method called De Novo programming for redesigning systems. Zeleny believed that most resources can be acquired at a reasonable price and thus that the only constraint is the total budget required to purchase those resources (Babic and Pavic 1996). Thus, the main difference between De Novo programming and traditional MODM is that De Novo programming reallocates the resources of a redesigned (or reshaped) system. With this system, the objective functions are subject to existing constraints and can eliminate the tradeoffs to achieve a solution that is considered ideal (i.e., an ideal point) in the context of the reconstructed decision space. The aforementioned theories and methods of MADM and MODM can contribute to solving traditional MCDM problems. The latest developments in MCDM are introduced in Chapter 2.
1.2 Statistics versus MCDM Approach
To understand the strengths and limitations of MCDM, one can distinguish the differences between statistical and MCDM approaches. Researchers who study social science topics usually depend on statistics as a major analytical tool and seek to generalize from sample data collected from a population. The fundamental assumptions of the statistical approach, such as the assumed probabilistic distributions of data sets and the independence of variables, are unrealistic and unsuitable for certain real-world problems with complex and interrelated variables, attributes, and criteria (Liou and Tzeng 2012; Liou 2013; Shen and Tzeng 2015a). Furthermore, MCDM studies are often aimed at solving a predefined problem; therefore, more emphasis is placed on constructing models that may be close to DMs’ preferences, and yield ideal or satisfactory guidance for decisions. MCDM may select an alternative with the highest preference rating or allocate existing resources efficiently based on the given constraints. For numerous widely adopted statistical methods and models, such as regressions and structural equation modeling, the statistical models’ assumptions would influence the analytical results. Consider a multiple regression model that explains the performance of suppliers by using several variables (e.g., workforce quality and operational efficiency); the performance of suppliers would be defined as a response variable y, and the explanatory variables xj (where j is the number of explanatory variables) are assumed to be independent. If n observations are available and each observation’s response value is indicated as yi (for i=1,…,n), then yi is assumed to be collected from a distribution with theoretical mean μi. In addition, yi would be conceptualized as μi + εi in the regression, where εi represents the effect of random errors; again, εi is assumed to be generated independently from a normal distribution with zero mean and a specific variation. In the addressed vendor selection model, the assumption for the probabilistic distribution of εi is neither identifiable nor examinable (Berk and Freeman 2003); however, it has certain effects on the obtained regression model.
In addition, the independence assumption of the explanatory variables xj is dubious in most social science problems. In the assumed case of supplier selection, the quality of a supplier’s workforce should have certain degree of influence on its operational efficiency; nevertheless, statistics requires that those two explanatory variables (i.e., workforce quality and operational efficiency) must be assumed to be independent. As mentioned, a research project based on statistics attempts to generalize its models to support its hypotheses and theories; consequently, such projects must collect data samples that are sufficiently large to be representative for the assumed population, which can only provide averaged numbers (Spronk et al. 2005) from the sample data. Such averaged results can describe or explain the relationships among the explanatory and response variables. By contrast, MCDM studies often address a predefined case in which DMs attempt to select the optimal decision (ranking or resource allocation). In contrast to the statistical approach, the MCDM approach avoids questionable probabilistic assumptions and seeks to solve problems. Consider how these two approaches would form the strategy of a large scale company (e.g., Microsoft or Apple) as an example. The statistical approach would tend to collect questionnaires from all available employees or shareholders to determine the average opinion, but the MCDM approach would query the preferences, knowledge, and experience of the managers of the company to devise an optimal strategy. Thus, we may roughly conclude that, the statistical approach puts more emphasis on examining the relationships among the variables for theoretical purposes, whereas the MCDM approach focuses on supporting DMs who must solve complicated decision problems in practice.
1.3 History of MADM
When von Neumann and Morgenstern (1947) published a generalized mathematical theory to model the dynamics among the competitors or players in a complex socioeconomic environment, their ideas marked the origin of MADM (Köksalan et al. 2011). This general theory provided various quantitative models with which researchers were able to tackle complicated decision problems. Early advances in MADM developed three major avenues: utility-based approaches, outranking methods, and pairwise comparison approaches. At present, MADM continues to grow rapidly and has incorporated multidisciplinary theories, methodologies, and techniques such as applied mathematics and information science.
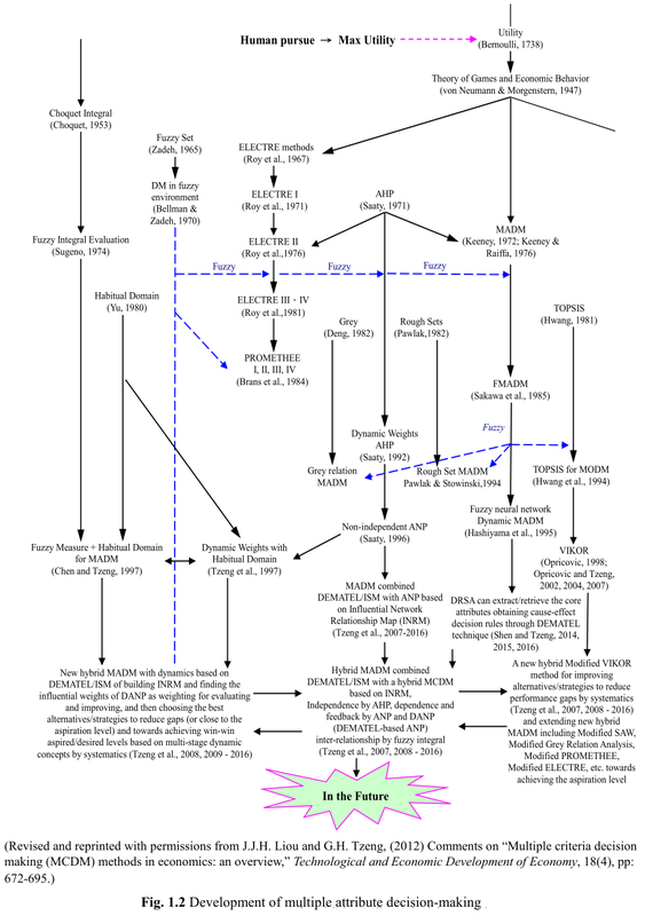
Because, as stated in Subsection 1.1, MADM considers DM preferences regarding multiple attributes, it can benefit from theories of utility that have been developed in economics. The initial attempt was MAUT (Keeney and Raiffa 1972, 1976), which was based on the utility theory from Bernoulli (1738). MAUT attempts to model DM preferences in a hierarchical structure by using various utility functions. Conjoint measurement is a key concern that utility-based methods address by aggregating the multiple values of various attributes with different scales to form a final utility value; numerous pioneering works have addressed this issue (Bouyssou and Pirlot 2005). Although early utility-based methods (e.g., MAUT and UTA) proposed certain techniques to resolve conjoint measurement, the major concern was and is the assumed independence among criteria, which is also termed “preferential independence” (Grabisch 1995; Hillier 2001). In numerous real-world problems, especially social problems, the preferential outcome of one criterion over another criterion is often influenced by the other criteria. Therefore, nonadditive type aggregators, such as the Choquet integral (Choquet, 1953) and fuzzy integral (Sugeno, 1974) aggregations, have been proposed for measuring the interactions among criteria. However, forming an adequate fuzzy measurement for those nonadditive type aggregators was and remains a challenging task in practice (Tzeng and Huang 2011; Liou et al. 2014). The historical development of MADM is shown in Fig 1.2.
1.1 Overview of Traditional MCDM Techniques and Methods
The goals of traditional decision-making can be sorted into several categories: ranking, selection, and optimization. A typical MCDM problem usually begins with identifying the goal and the related criteria, attributes, or constraints. Subsequently, to evaluate the available alternative solutions to a problem, researchers must collect the preferences of the decision makers (DMs) regarding the available alternatives in the context of the pertinent criteria. If only a single criterion (or attribute) were considered, it would be intuitive to choose the alternative with the highest preference rating. In the presence of multiple criteria (or attributes), DMs are usually compelled to compromise among a group of alternatives even though none of the alternatives outperforms or dominates the others on all the criteria. Therefore, various quantitative methods have been proposed to support DMs who must make decisions that advance predefined goals.
Following Hwang and Yoon (1981), MCDM problems can be further categorized into two subfields: multiple attribute decision-making (MADM) and multiple objective decision-making (MODM); MADM is concerned with ranking or selecting by evaluating predetermined alternatives, and MODM is aimed at identifying the optimal outcome by searching for an efficient frontier within a solution space under the given constraints. Most conventional MCDM research comprises these two subfields of MADM and MODM (Köksalan et al. 2011).
Because MADM focuses on evaluating alternatives according to a DM’s preference, it is reasonable to adopt the utility theory from economics to depict a DM’s preferences for multiple attributes in the form of preference (value or utility) functions; this is performed in multiple attribute utility theory (MAUT). Although MAUT has solid foundations from economic theories, its essential assumption is based on the independence of attributes, which is not realistic in most real-world cases. The utility additive (UTA) method extends the MAUT method and uses regression and linear programming techniques to reach the solution of optimal value (utility) that is consistent with a DM’s global preferences. However, just as MAUT assumes the independence of attributes, UTA methods assume the independence of variables (i.e., attributes or criteria).
Another prevalent approach in MADM research is the analytic hierarchy process (AHP), which was introduced by Saaty (1972, 1992). AHP decomposes a problem into hierarchical levels (mainly dealing with two levels: dimensions and criteria), and uses pairwise comparisons to calculate a DM’s global preferences regarding the final goal. Certain aggregation methods (additive type operators), such as SAW, TOPSIS, VIKOR, and PROMETHEE, may integrate with the preference weights obtained by traditional MADM methods in order to support DMs who must make the final ranking or selection. MADM methods are mainly devised for evaluations.
By contrast, MODM is more suitable for designing or planning by optimizing the allocation of limited resources. Because real-world environments are often full of competing and even conflicting constraints, DMs may rely on MODM methods to achieve multiple goals simultaneously; mathematical programming is mainly adopted to solve those optimization problems. Nevertheless, traditional MODM optimization methods are only concerned with Pareto optimal solutions (also called non-inferior non-dominated solutions or effective solutions) within a system; notions of essential optimization are not addressed (Zeleny 1990). When encountering an MODM problem, DMs usually find that optimization of all objectives in a given system is impossible. Most problems involve tradeoffs; one cannot increase the levels of satisfaction for one objective without reducing those for another. Conventional multiobjective programming techniques are often applied to search for non-inferior solutions (i.e., Pareto optimal solutions) or compromise solutions, which are transformed into single-objective programs that produce solutions acceptable to DMs. When objective functions conflict with one another, DMs can formalize tradeoffs by using conventional methods.
Because tradeoffs often prevent the simultaneous optimization of all criteria, Zeleny (1982) offered an MODM method called De Novo programming for redesigning systems. Zeleny believed that most resources can be acquired at a reasonable price and thus that the only constraint is the total budget required to purchase those resources (Babic and Pavic 1996). Thus, the main difference between De Novo programming and traditional MODM is that De Novo programming reallocates the resources of a redesigned (or reshaped) system. With this system, the objective functions are subject to existing constraints and can eliminate the tradeoffs to achieve a solution that is considered ideal (i.e., an ideal point) in the context of the reconstructed decision space. The aforementioned theories and methods of MADM and MODM can contribute to solving traditional MCDM problems. The latest developments in MCDM are introduced in Chapter 2.
1.2 Statistics versus MCDM Approach
To understand the strengths and limitations of MCDM, one can distinguish the differences between statistical and MCDM approaches. Researchers who study social science topics usually depend on statistics as a major analytical tool and seek to generalize from sample data collected from a population. The fundamental assumptions of the statistical approach, such as the assumed probabilistic distributions of data sets and the independence of variables, are unrealistic and unsuitable for certain real-world problems with complex and interrelated variables, attributes, and criteria (Liou and Tzeng 2012; Liou 2013; Shen and Tzeng 2015a). Furthermore, MCDM studies are often aimed at solving a predefined problem; therefore, more emphasis is placed on constructing models that may be close to DMs’ preferences, and yield ideal or satisfactory guidance for decisions. MCDM may select an alternative with the highest preference rating or allocate existing resources efficiently based on the given constraints. For numerous widely adopted statistical methods and models, such as regressions and structural equation modeling, the statistical models’ assumptions would influence the analytical results. Consider a multiple regression model that explains the performance of suppliers by using several variables (e.g., workforce quality and operational efficiency); the performance of suppliers would be defined as a response variable y, and the explanatory variables xj (where j is the number of explanatory variables) are assumed to be independent. If n observations are available and each observation’s response value is indicated as yi (for i=1,…,n), then yi is assumed to be collected from a distribution with theoretical mean μi. In addition, yi would be conceptualized as μi + εi in the regression, where εi represents the effect of random errors; again, εi is assumed to be generated independently from a normal distribution with zero mean and a specific variation. In the addressed vendor selection model, the assumption for the probabilistic distribution of εi is neither identifiable nor examinable (Berk and Freeman 2003); however, it has certain effects on the obtained regression model.
In addition, the independence assumption of the explanatory variables xj is dubious in most social science problems. In the assumed case of supplier selection, the quality of a supplier’s workforce should have certain degree of influence on its operational efficiency; nevertheless, statistics requires that those two explanatory variables (i.e., workforce quality and operational efficiency) must be assumed to be independent. As mentioned, a research project based on statistics attempts to generalize its models to support its hypotheses and theories; consequently, such projects must collect data samples that are sufficiently large to be representative for the assumed population, which can only provide averaged numbers (Spronk et al. 2005) from the sample data. Such averaged results can describe or explain the relationships among the explanatory and response variables. By contrast, MCDM studies often address a predefined case in which DMs attempt to select the optimal decision (ranking or resource allocation). In contrast to the statistical approach, the MCDM approach avoids questionable probabilistic assumptions and seeks to solve problems. Consider how these two approaches would form the strategy of a large scale company (e.g., Microsoft or Apple) as an example. The statistical approach would tend to collect questionnaires from all available employees or shareholders to determine the average opinion, but the MCDM approach would query the preferences, knowledge, and experience of the managers of the company to devise an optimal strategy. Thus, we may roughly conclude that, the statistical approach puts more emphasis on examining the relationships among the variables for theoretical purposes, whereas the MCDM approach focuses on supporting DMs who must solve complicated decision problems in practice.
1.3 History of MADM
When von Neumann and Morgenstern (1947) published a generalized mathematical theory to model the dynamics among the competitors or players in a complex socioeconomic environment, their ideas marked the origin of MADM (Köksalan et al. 2011). This general theory provided various quantitative models with which researchers were able to tackle complicated decision problems. Early advances in MADM developed three major avenues: utility-based approaches, outranking methods, and pairwise comparison approaches. At present, MADM continues to grow rapidly and has incorporated multidisciplinary theories, methodologies, and techniques such as applied mathematics and information science.
Because, as stated in Subsection 1.1, MADM considers DM preferences regarding multiple attributes, it can benefit from theories of utility that have been developed in economics. The initial attempt was MAUT (Keeney and Raiffa 1972, 1976), which was based on the utility theory from Bernoulli (1738). MAUT attempts to model DM preferences in a hierarchical structure by using various utility functions. Conjoint measurement is a key concern that utility-based methods address by aggregating the multiple values of various attributes with different scales to form a final utility value; numerous pioneering works have addressed this issue (Bouyssou and Pirlot 2005). Although early utility-based methods (e.g., MAUT and UTA) proposed certain techniques to resolve conjoint measurement, the major concern was and is the assumed independence among criteria, which is also termed “preferential independence” (Grabisch 1995; Hillier 2001). In numerous real-world problems, especially social problems, the preferential outcome of one criterion over another criterion is often influenced by the other criteria. Therefore, nonadditive type aggregators, such as the Choquet integral (Choquet, 1953) and fuzzy integral (Sugeno, 1974) aggregations, have been proposed for measuring the interactions among criteria. However, forming an adequate fuzzy measurement for those nonadditive type aggregators was and remains a challenging task in practice (Tzeng and Huang 2011; Liou et al. 2014). The historical development of MADM is shown in Fig 1.2.
The outranking methods, especially the ELECTRE families (Benayoun et al. 1966; Roy 1968) and PROMETHEE families (Brans et al. 1984), compare the preference relations among alternatives to acquire information regarding the optimal alternative. Although empirical outranking methods were proposed for overcoming the practical difficulties experienced with utility functions, outranking methods have been criticized for their lack of axiomatic foundations, particularly for classical aggregation problems, structural problems, and noncompensatory problems (Bouyssou and Vansnick 1986). In addition, the outranking approach requires DMs to pass subjective judgments regarding the performance of each alternative on each criterion. Each weight on each criterion must be assigned before the outranking decision model can be formed. Although each criterion has a different scale, DMs are expected to give consistent and precise judgments on the relative importance of weight. The synthesized utility function must be calculated from a partial set of pairwise comparisons between alternatives, and direct comparisons present difficulties if the number of criteria is large. Unfortunately, practical problems in complicated social or business settings often must account for numerous criteria.
In 1965, fuzzy set theory (Zadeh 1965; Bellman and Zadeh 1970) was proposed to confront the problems of linguistic definitions and uncertain information. Fuzzy sets generalize conventional set theory. Fuzzy sets have enriched the field of automatic control. Since the 1970s, MADM has applied fuzzy sets to situations of subjective uncertainty.
The third approach forms evaluation models by using pairwise comparisons of attributes or criteria from DMs. This approach has the advantage of requiring each DM to focus on only two criteria or attributes at a time, which streamlines complex analyses. According to the theory that human brains are constrained by bounded rationality (Simon 1972, 1982), pairwise comparisons should assist DMs to provide precise opinions. In contrast to the outranking approach, the pairwise comparison approach can usefully evaluate the relative weights of criteria—even when considering a large number of criteria. Because the third approach also relies heavily on retrieving and transforming experts’ or DMs’ opinions or judgments to form evaluation models, the impreciseness and uncertainty of those opinions or judgments cannot be overlooked; it is reasonable to incorporate the fuzzy set theory to enhance pairwise comparison methods (Sakawa and Yano 1985; Tzeng and Huang 2011).
The widely adopted AHP (Saaty 1988) was based on the assumption of independent criteria, but the generalized analytic network process (ANP) (Saaty 1996) allows for interrelationships among criteria. ANP has been applied to various decision problems in fields such as science, military operations, engineering, and socioeconomics. According to a recent survey of journals from Mardani et al. (2015), except for hybrid fuzzy MADM methods, AHP and ANP methods might be the most prevalent type of MADM research published over the past 20 years.
1.4 History of MODM
MODM aims to solve optimization problems under specified constraints. In these problems, several (conflicting) objectives must be achieved simultaneously. Traditional MODM adopts mathematical programming to identify the optimal (ideal) solution, but traditional MODM must address two major issues: (1) tradeoffs among objectives and (2) scale problems, which are sometimes termed “the curse of dimensionality.”
First, the tradeoff problem arises from the conflicts among the objectives; to resolve this issue, the tradeoffs between the considered objectives can be identified and multiple objectives can be transformed into a weighted single objective to simplify the original problem. Second, the scaling problem arises when increases in the number of relevant dimensions or criteria cause the computational cost to increase tremendously. The scale problem was considered to be a major challenge to the mainframes of the 1950s and 1960s, but since the late 1980s, personal computers have provided ample computational resources to general researchers. In addition, certain evolutionary techniques, such as genetic algorithms (GAs) (Holland 1975) and particle swarm optimization (PSO) (Coello et al. 2004) have increased the efficiency of searches in solution spaces.
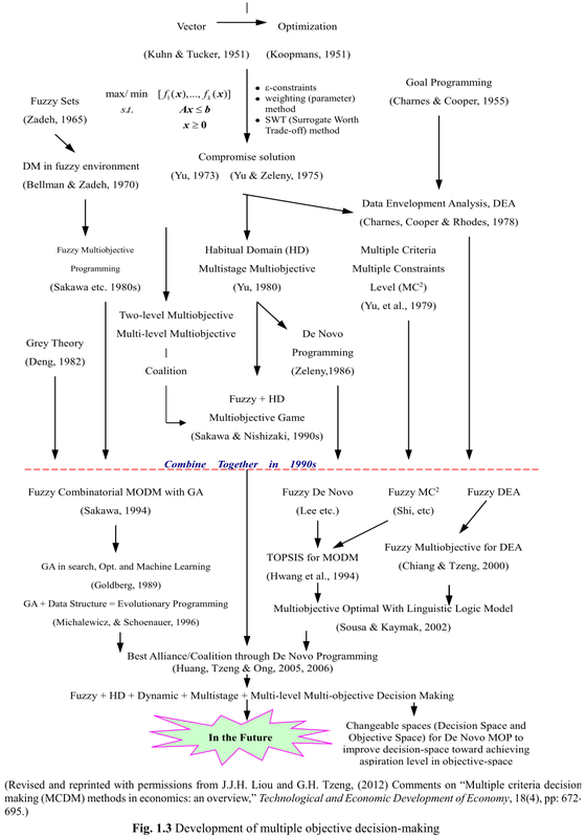
As shown in Fig 1.3, the concept of vector optimization (Kuhn and Tucker 1951) might be considered to be the beginning of MODM. After Yu (1973) proposed the compromise solution method to cope with MODM problems, various applications began to grow rapidly, such as transportation investment, transportation planning, econometrics, development planning, financial planning, business administration, investment portfolio selection, land-use planning, water resource management, public policy, and environmental issues.
Although the main body of traditional MODM methods was extended from simple MOP to multilevel multiobjective programming and multistage multiobjective programming in the 1980s, soft computing, such as fuzzy set theory (Zadeh 1965) and grey theory (Deng 1982), and goal programming, such as data envelopment analysis (DEA) (Charnes et al. 1978), also emerged and began to be incorporated with certain MODM methods for investigating real-world problems.
The uncertainty of real-world environments and the subjective nature of DM judgments cause soft computing techniques (like fuzzy set theory) to play an influential role in MODM. Objectives and constraints may be provided in the form of natural language terms (e.g., low debt ratio), and fuzzy numbers (variables) are often advantageous to represent the uncertainty or impreciseness underlying MODM models. Ever since Bellman and Zadeh (1970) proposed various concepts of decision-making under fuzzy environments, MADM and MODM researchers have appreciated the effectiveness of fuzzy set theory. Systematic discussions on fuzzy MODM can be found in previous works such as Hwang and Yoon (1981), Zimmermann (1978), Sakawa et al. (1984), Lee and Li (1993), and Tzeng and Huang (2013).
DEA might be the most prevalent goal programming method; it has been widely used to measure the technical efficiency of decision-making units (DMUs). Unlike regression-based methods, DEA is a nonparametric approach and is more suitable for resolving practical problems (Tzeng and Huang, 2013) without dubious assumptions concerning parameters in a model.
The first DEA method was the famous CCR model (by Charnes, Cooper, and Rhodes), which can evaluate the efficiency and inefficiency of DMUs by converting multiple inputs into multiple outputs through mathematical programming techniques. Subsequently, network DEA (Fare and Grosskopf 1997, 2012) extended classical DEA by forming the network relationships and models that consider subunits of DMUs as basic DEA units. A considerable number of studies (e.g., Tone and Tsutsui 2009, 2014; Cook et al. 2010) in management sciences and economics have evaluated the performance of DMUs and have sought to improve underperforming DMUs. In the 1990s, DEA incorporated fuzzy set theory for capturing the uncertainty and impreciseness in MOP; one example is the bisection method proposed by Sakawa and Yumine (1983), which outperformed nonlinear programming with fuzzy set theory in MOP. Certain fuzzy MOP studies have continued this trend (Chiang and Tzeng 2000; Tzeng and Huang 2013). The holistic development of MODM is illustrated in Fig 1.3.
Recently MODM has gradually shifted from win–lose strategies to win–win strategies (Tzeng and Huang 2013). A win–lose strategy means a firm can only optimize its system by using the given resources and restricted capabilities. That is, the firm faces traditional optimization problems. Increasing numbers of firms seek to create added value and achieve new heights of performance through flexible resources and expanding competencies. Those new concepts and developments in MODM are discussed in the first part of this book.
In 1965, fuzzy set theory (Zadeh 1965; Bellman and Zadeh 1970) was proposed to confront the problems of linguistic definitions and uncertain information. Fuzzy sets generalize conventional set theory. Fuzzy sets have enriched the field of automatic control. Since the 1970s, MADM has applied fuzzy sets to situations of subjective uncertainty.
The third approach forms evaluation models by using pairwise comparisons of attributes or criteria from DMs. This approach has the advantage of requiring each DM to focus on only two criteria or attributes at a time, which streamlines complex analyses. According to the theory that human brains are constrained by bounded rationality (Simon 1972, 1982), pairwise comparisons should assist DMs to provide precise opinions. In contrast to the outranking approach, the pairwise comparison approach can usefully evaluate the relative weights of criteria—even when considering a large number of criteria. Because the third approach also relies heavily on retrieving and transforming experts’ or DMs’ opinions or judgments to form evaluation models, the impreciseness and uncertainty of those opinions or judgments cannot be overlooked; it is reasonable to incorporate the fuzzy set theory to enhance pairwise comparison methods (Sakawa and Yano 1985; Tzeng and Huang 2011).
The widely adopted AHP (Saaty 1988) was based on the assumption of independent criteria, but the generalized analytic network process (ANP) (Saaty 1996) allows for interrelationships among criteria. ANP has been applied to various decision problems in fields such as science, military operations, engineering, and socioeconomics. According to a recent survey of journals from Mardani et al. (2015), except for hybrid fuzzy MADM methods, AHP and ANP methods might be the most prevalent type of MADM research published over the past 20 years.
1.4 History of MODM
MODM aims to solve optimization problems under specified constraints. In these problems, several (conflicting) objectives must be achieved simultaneously. Traditional MODM adopts mathematical programming to identify the optimal (ideal) solution, but traditional MODM must address two major issues: (1) tradeoffs among objectives and (2) scale problems, which are sometimes termed “the curse of dimensionality.”
First, the tradeoff problem arises from the conflicts among the objectives; to resolve this issue, the tradeoffs between the considered objectives can be identified and multiple objectives can be transformed into a weighted single objective to simplify the original problem. Second, the scaling problem arises when increases in the number of relevant dimensions or criteria cause the computational cost to increase tremendously. The scale problem was considered to be a major challenge to the mainframes of the 1950s and 1960s, but since the late 1980s, personal computers have provided ample computational resources to general researchers. In addition, certain evolutionary techniques, such as genetic algorithms (GAs) (Holland 1975) and particle swarm optimization (PSO) (Coello et al. 2004) have increased the efficiency of searches in solution spaces.
As shown in Fig 1.3, the concept of vector optimization (Kuhn and Tucker 1951) might be considered to be the beginning of MODM. After Yu (1973) proposed the compromise solution method to cope with MODM problems, various applications began to grow rapidly, such as transportation investment, transportation planning, econometrics, development planning, financial planning, business administration, investment portfolio selection, land-use planning, water resource management, public policy, and environmental issues.
Although the main body of traditional MODM methods was extended from simple MOP to multilevel multiobjective programming and multistage multiobjective programming in the 1980s, soft computing, such as fuzzy set theory (Zadeh 1965) and grey theory (Deng 1982), and goal programming, such as data envelopment analysis (DEA) (Charnes et al. 1978), also emerged and began to be incorporated with certain MODM methods for investigating real-world problems.
The uncertainty of real-world environments and the subjective nature of DM judgments cause soft computing techniques (like fuzzy set theory) to play an influential role in MODM. Objectives and constraints may be provided in the form of natural language terms (e.g., low debt ratio), and fuzzy numbers (variables) are often advantageous to represent the uncertainty or impreciseness underlying MODM models. Ever since Bellman and Zadeh (1970) proposed various concepts of decision-making under fuzzy environments, MADM and MODM researchers have appreciated the effectiveness of fuzzy set theory. Systematic discussions on fuzzy MODM can be found in previous works such as Hwang and Yoon (1981), Zimmermann (1978), Sakawa et al. (1984), Lee and Li (1993), and Tzeng and Huang (2013).
DEA might be the most prevalent goal programming method; it has been widely used to measure the technical efficiency of decision-making units (DMUs). Unlike regression-based methods, DEA is a nonparametric approach and is more suitable for resolving practical problems (Tzeng and Huang, 2013) without dubious assumptions concerning parameters in a model.
The first DEA method was the famous CCR model (by Charnes, Cooper, and Rhodes), which can evaluate the efficiency and inefficiency of DMUs by converting multiple inputs into multiple outputs through mathematical programming techniques. Subsequently, network DEA (Fare and Grosskopf 1997, 2012) extended classical DEA by forming the network relationships and models that consider subunits of DMUs as basic DEA units. A considerable number of studies (e.g., Tone and Tsutsui 2009, 2014; Cook et al. 2010) in management sciences and economics have evaluated the performance of DMUs and have sought to improve underperforming DMUs. In the 1990s, DEA incorporated fuzzy set theory for capturing the uncertainty and impreciseness in MOP; one example is the bisection method proposed by Sakawa and Yumine (1983), which outperformed nonlinear programming with fuzzy set theory in MOP. Certain fuzzy MOP studies have continued this trend (Chiang and Tzeng 2000; Tzeng and Huang 2013). The holistic development of MODM is illustrated in Fig 1.3.
Recently MODM has gradually shifted from win–lose strategies to win–win strategies (Tzeng and Huang 2013). A win–lose strategy means a firm can only optimize its system by using the given resources and restricted capabilities. That is, the firm faces traditional optimization problems. Increasing numbers of firms seek to create added value and achieve new heights of performance through flexible resources and expanding competencies. Those new concepts and developments in MODM are discussed in the first part of this book.
1.5 Developments of Computational Machine and Soft Computing for Decision Aids
In the 1950s and 1960s, MCDM researchers attempted to develop mathematical models and methods to support DMs who made decisions concerning ranking, selection, or optimization (see Fig 1.3). The early digital computers of the 1950s were large and expensive vacuum tube machines that were not easily accessed or used by researchers. Consequently, early MCDM studies did not expect to leverage digital computational resources to resolve complicated decision problems. In the 1970s, as transistors began to replace vacuum tubes, and in the 1980s, when affordable integrated circuits provided billions of transistors on a single chip, low-cost and convenient computational power gave researchers the opportunity to devise complicated algorithms to enhance the quality of decisions. In the present text, we mainly discuss three subfields of computer science that have influenced MCDM research over the past several decades: (1) computer-supported linear programming; (2) machine learning in computational intelligence; and (3) soft computing techniques.
First, computer-supported linear programming techniques have been adopted to solve optimization problems in operational research and MODM since the Second World War. Famous software packages, such as Lingo and the Solver module of Excel, have been used widely to solve the aforementioned MODM problems in various fields. Consider the following typical MODM problem:
In the 1950s and 1960s, MCDM researchers attempted to develop mathematical models and methods to support DMs who made decisions concerning ranking, selection, or optimization (see Fig 1.3). The early digital computers of the 1950s were large and expensive vacuum tube machines that were not easily accessed or used by researchers. Consequently, early MCDM studies did not expect to leverage digital computational resources to resolve complicated decision problems. In the 1970s, as transistors began to replace vacuum tubes, and in the 1980s, when affordable integrated circuits provided billions of transistors on a single chip, low-cost and convenient computational power gave researchers the opportunity to devise complicated algorithms to enhance the quality of decisions. In the present text, we mainly discuss three subfields of computer science that have influenced MCDM research over the past several decades: (1) computer-supported linear programming; (2) machine learning in computational intelligence; and (3) soft computing techniques.
First, computer-supported linear programming techniques have been adopted to solve optimization problems in operational research and MODM since the Second World War. Famous software packages, such as Lingo and the Solver module of Excel, have been used widely to solve the aforementioned MODM problems in various fields. Consider the following typical MODM problem:
In Eq. (1.1), fi(x) denotes the ith goal that must be maximized, and x is a matrix of multiple constraints, all of which must be satisfied. Suppose the number of goals is 10 (i.e., n=10) and the number of constraints is 100 with 50 variables; it would be nearly impossible to solve this problem without the use of computer-supported linear programming techniques. Because the modern social and business environments have grown greatly in complexity, typical real-world problems must consider numerous goals, constraints, and variables in practice. Since the 1980s, to maximize the efficiency of computational resource utilization, linear programming techniques have been combined with certain evolutionary computing techniques (e.g., GA) to search for optimal results (e.g., Goldberg 1989). The latest developments and newest concepts in this research thread are discussed in Chapter 2.
Second, although the distinction between computational intelligence and artificial intelligence (AI) is not always clear, computational intelligence is often regarded as a complementary field to AI in computer science (Eiben and Smith 2003), and those two fields both attempt to generate intelligent outputs or intelligent actions based on the calculations of machines. The term “AI” originated from the proposal of McCarthy and others in 1955, and a major goal of AI (in the long term) is to create an intelligent machine with the thinking capability to learn and sense with consciousness; this ambitious goal remains controversial in certain respects (such as in its philosophy, psychology, and ethics). AI mainly concerns multidisciplinary knowledge-based approaches from various fields. The discipline of computational intelligence applies computers or specialized hardware to prediction and pattern classification problems; in here, we discuss only the machine learning techniques in computational intelligence that have been applied in MCDM research. Interested readers may refer to the work edited by Doumpos and Grigoroundis (2013) for a more comprehensive discussion.
Machine learning techniques have strengths in analyzing the nonlinear relationships in data, and most machine learning techniques (e.g., artificial neural networks (ANNs), decision trees (DTs), and support vector machines (SVMs)) are not required to assume any probabilistic distribution of data. Classifiers are machine learning techniques that learn from historical data to provide predictive outcomes for DMs as decision aids. ANN-related techniques (e.g., back-propagation, self-organizing map ANNs, and competitive learning neural networks) might have been the most prevalent techniques for solving prediction problems (such as the financial market prediction) over the past several decades (Lin et al. 2012). ANN techniques mimic the learning mechanism of brains, and the learned results are stored in the connections between neurons; because it is difficult to extract comprehensible meaning from the ANN learning process and the learned results, they are often criticized as a “black box” (Shen and Tzeng 2014a). Some other single classifiers, such as SVMs (Wang et al. 2005) and random forests, also suffer from similar drawbacks. To enhance the classification accuracy of single classifiers, hybrid classifiers combine two or more techniques [e.g., GA+SVM (Huang et al. 2006) and DT+ANN+SVM (Hung and Chen 2009)]. In such a hybrid system, one technique performs the initial classification, and the others tune some of the parameters of the hybrid models (GAs or ANNs are often adopted to optimize the parameters during the learning phase). Generally, machine learning techniques focus on increasing the accuracy of classification or prediction.
Some machine learning techniques that learn from decision examples have been proposed to form the preference weights for MADM models. For example, Malakooti and Zhou (1994) used ANNs for formulating and assessing utility functions by eliciting information from DMs, and the trained ANN models were adopted to rank alternatives. Several recent studies in MCDM could be categorized as part of this approach (Taha and Rostam 2011), but academic interest in this approach seems to have waned gradually. Aside from machine learning techniques, evolutionary computing methods (e.g., GA and PSO), mentioned in Subsection 1.3, have been widely integrated with linear programming techniques for solving complex optimization problems. Evolutionary computing algorithms emulate natural evolutionary processes, which are mainly used in MODM studies (Tzeng and Huang 2013).
Third, soft computing techniques, particularly fuzzy sets (Zadeh 1965) and rough sets (Pawlak 1982), are based on solid mathematical foundations to model the impreciseness or uncertainty in a system, and have been widely applied in engineering (Zimmermann 2001) and social economics (Tzeng and Huang 2011, 2013). One of the key advantages of soft computing techniques is that meaningful logic or rules can be obtained for the addressed problem. Soft computing techniques are often integrated with machine learning techniques to maximize accuracy. For example, fuzzy inference was integrated with ANNs to form an adaptive-network-based fuzzy inference system (Jang 1993), which was used to support the financial predictions of commercial banks (Shen and Tzeng 2014a). We briefly introduce the essential ideas of these two soft computing techniques in Subsections 1.5.1 and 1.5.2.
1.5.1 Basic Concepts of Fuzzy Sets
Fuzzy set theory (Zadeh 1965) was proposed to denote the degrees to which particular elements can be said to belong to specific sets; therefore, fuzzy set calculations require greater computational resources than crisp sets do. Fuzzy set theory has been an emerging field of applied mathematics since the 1970s, and the extended subfields of fuzzy sets include fuzzy relations, fuzzy graphs, fuzzy clustering, fuzzy inference (fuzzy logic), and fuzzy linguistics. Among the aforementioned subfields of fuzzy sets theory, fuzzy linguistics and fuzzy ranking (which is based on fuzzy linguistics) play the most influential roles in MCDM research. This helps collect DMs’ imprecise judgments to form an adequate preference model. The fundamental notions of the fuzzy sets could be expressed as follows.
Second, although the distinction between computational intelligence and artificial intelligence (AI) is not always clear, computational intelligence is often regarded as a complementary field to AI in computer science (Eiben and Smith 2003), and those two fields both attempt to generate intelligent outputs or intelligent actions based on the calculations of machines. The term “AI” originated from the proposal of McCarthy and others in 1955, and a major goal of AI (in the long term) is to create an intelligent machine with the thinking capability to learn and sense with consciousness; this ambitious goal remains controversial in certain respects (such as in its philosophy, psychology, and ethics). AI mainly concerns multidisciplinary knowledge-based approaches from various fields. The discipline of computational intelligence applies computers or specialized hardware to prediction and pattern classification problems; in here, we discuss only the machine learning techniques in computational intelligence that have been applied in MCDM research. Interested readers may refer to the work edited by Doumpos and Grigoroundis (2013) for a more comprehensive discussion.
Machine learning techniques have strengths in analyzing the nonlinear relationships in data, and most machine learning techniques (e.g., artificial neural networks (ANNs), decision trees (DTs), and support vector machines (SVMs)) are not required to assume any probabilistic distribution of data. Classifiers are machine learning techniques that learn from historical data to provide predictive outcomes for DMs as decision aids. ANN-related techniques (e.g., back-propagation, self-organizing map ANNs, and competitive learning neural networks) might have been the most prevalent techniques for solving prediction problems (such as the financial market prediction) over the past several decades (Lin et al. 2012). ANN techniques mimic the learning mechanism of brains, and the learned results are stored in the connections between neurons; because it is difficult to extract comprehensible meaning from the ANN learning process and the learned results, they are often criticized as a “black box” (Shen and Tzeng 2014a). Some other single classifiers, such as SVMs (Wang et al. 2005) and random forests, also suffer from similar drawbacks. To enhance the classification accuracy of single classifiers, hybrid classifiers combine two or more techniques [e.g., GA+SVM (Huang et al. 2006) and DT+ANN+SVM (Hung and Chen 2009)]. In such a hybrid system, one technique performs the initial classification, and the others tune some of the parameters of the hybrid models (GAs or ANNs are often adopted to optimize the parameters during the learning phase). Generally, machine learning techniques focus on increasing the accuracy of classification or prediction.
Some machine learning techniques that learn from decision examples have been proposed to form the preference weights for MADM models. For example, Malakooti and Zhou (1994) used ANNs for formulating and assessing utility functions by eliciting information from DMs, and the trained ANN models were adopted to rank alternatives. Several recent studies in MCDM could be categorized as part of this approach (Taha and Rostam 2011), but academic interest in this approach seems to have waned gradually. Aside from machine learning techniques, evolutionary computing methods (e.g., GA and PSO), mentioned in Subsection 1.3, have been widely integrated with linear programming techniques for solving complex optimization problems. Evolutionary computing algorithms emulate natural evolutionary processes, which are mainly used in MODM studies (Tzeng and Huang 2013).
Third, soft computing techniques, particularly fuzzy sets (Zadeh 1965) and rough sets (Pawlak 1982), are based on solid mathematical foundations to model the impreciseness or uncertainty in a system, and have been widely applied in engineering (Zimmermann 2001) and social economics (Tzeng and Huang 2011, 2013). One of the key advantages of soft computing techniques is that meaningful logic or rules can be obtained for the addressed problem. Soft computing techniques are often integrated with machine learning techniques to maximize accuracy. For example, fuzzy inference was integrated with ANNs to form an adaptive-network-based fuzzy inference system (Jang 1993), which was used to support the financial predictions of commercial banks (Shen and Tzeng 2014a). We briefly introduce the essential ideas of these two soft computing techniques in Subsections 1.5.1 and 1.5.2.
1.5.1 Basic Concepts of Fuzzy Sets
Fuzzy set theory (Zadeh 1965) was proposed to denote the degrees to which particular elements can be said to belong to specific sets; therefore, fuzzy set calculations require greater computational resources than crisp sets do. Fuzzy set theory has been an emerging field of applied mathematics since the 1970s, and the extended subfields of fuzzy sets include fuzzy relations, fuzzy graphs, fuzzy clustering, fuzzy inference (fuzzy logic), and fuzzy linguistics. Among the aforementioned subfields of fuzzy sets theory, fuzzy linguistics and fuzzy ranking (which is based on fuzzy linguistics) play the most influential roles in MCDM research. This helps collect DMs’ imprecise judgments to form an adequate preference model. The fundamental notions of the fuzzy sets could be expressed as follows.
In recent trends of MADM research, models that are based on the pairwise comparison approach (such as the aforementioned AHP and ANP) also adopt fuzzy sets to indicate the preference weights of the involved criteria in a decision model. These weights can be synthesized with the performance values based on the linguistic evaluation of an alternative for each criterion.
1.5.2 Basic Notions of Rough Sets
The basic notions of rough sets were introduced by Pawlak in the early 1980s after fuzzy set theory had been developed. Although fuzzy sets and rough sets were all devised to model impreciseness, rough set theory (RST) is more information-oriented. It is based on collecting vague patterns or knowledge from available data.
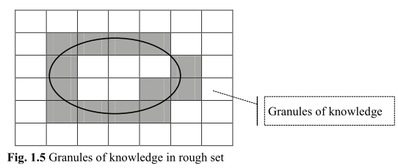
The essential idea of classical RST is the indiscernibility of the objects in the universe of discourse Ur, in the view of the available attributes about those objects. Any subset of all indiscernible objects is called an elementary set; an elementary set denotes a basic granule of knowledge about the universe. Any union of elementary sets is a crisp set; all other unions are rough sets. In the presence of rough sets in Ur, each rough set has boundary-line cases (defined by upper and lower approximations). Because RST assumes that objects can only be discerned through the information that can be gained about them from their observed attributes, RST regards knowledge as a granular structure. The basic notions of the granules of knowledge in a rough set are illustrated in Fig 1.5.
1.5.2 Basic Notions of Rough Sets
The basic notions of rough sets were introduced by Pawlak in the early 1980s after fuzzy set theory had been developed. Although fuzzy sets and rough sets were all devised to model impreciseness, rough set theory (RST) is more information-oriented. It is based on collecting vague patterns or knowledge from available data.
The essential idea of classical RST is the indiscernibility of the objects in the universe of discourse Ur, in the view of the available attributes about those objects. Any subset of all indiscernible objects is called an elementary set; an elementary set denotes a basic granule of knowledge about the universe. Any union of elementary sets is a crisp set; all other unions are rough sets. In the presence of rough sets in Ur, each rough set has boundary-line cases (defined by upper and lower approximations). Because RST assumes that objects can only be discerned through the information that can be gained about them from their observed attributes, RST regards knowledge as a granular structure. The basic notions of the granules of knowledge in a rough set are illustrated in Fig 1.5.
|
According to the defined upper and lower approximations and the boundary regions, RST may help reduce the required attributes (i.e., CORE attributes; the related discussion is provided in Subsection 1.6) to discern the target attribute (also termed decision attribute), which may support the minimal and representative attributes (criteria) for MADM models. 1.6 Emerging Trend in Multiple Rules-Based Decision-Making (MRDM) Extended from the classical RST, DRSA (Greco et al. 1999, 2002a, 2002b, 2005) was proposed to consider the preferential characteristics in attributes and the “dominance” relationships among alternatives (with respect to certain attributes in the system for classification). The idea of preference regarding criteria is crucial in decision-making. For example, in a stock selection problem, the alternative with higher profitability (which is a criterion) should be preferred. Thus, the potential usefulness of DRSA in resolving MCDM problems has been recognized since the late 1990s (Greco et al. 2001, 2005, 2008; Slowinski 2008). A new trend in MCDM has also emerged since then and may be termed multiple rule-based decision-making (MRDM); one of the key advantages of DRSA is that it can generate a set of decision rules to denote the rough knowledge in data. The basic ideas of DRSA are briefly discussed as follows. DRSA may begin with organizing data in IS in the form of a table, with the attributes and objects (alternatives) arranged in rows and columns, respectively. The table of DRSA is a 4-tuple IS, i.e.,
|
|
The high potential of DRSA as a decision aid in MCDM, for ranking or selection, has been noticed since the works of Greco et al. (1999, 2001, 2005), which has emerged as a new research field in MCDM. The original idea was based on collecting a certain preference order (i.e., partial preorder of the available alternatives in which a DM has confidence) and forming a pairwise comparison table (PCT), introduced by Greco et al. (1997, 1999). Subsequently, the dominance principle, stated as multigraded dominance by Slowinski et al. (2005) or as the dominance relation D2 by Szelag et al. (2013) is defined on pairs of objects, such as: if objects a, b, c, d ∈ U , (a, b) and (c, d) are defined as pairs over set H , pair (a, b) is regarded as D2 dominance (c, d) with respect to criteria P ⊆ C (where C is the aforementioned condition attribute set in DRSA, and P is a partial set of C ), iff Vi(a)- Vi(b) ≧ Vi(c) – Vi(d) for each criterion I ∈ P (in here, Vi(a) denotes the value of alternative a on criterion i). In the next, on the basis of the essential ideas of DRSA, decision rules were adopted for capturing the rough knowledge from the aforementioned PCT. The obtained decision rules are thus applied to the other alternatives (objects), and to certain exploitation methods, such as the net flow score of Greco et al. (1999). This can be adopted to give rankings for the whole set of alternatives. This approach enables ranking by collecting a set of reference objects to denote the preference structure of a DM. The obtained DRSA decision-rule-based exploitations are to be calculated for the preference order of all alternatives. It may be regarded as the multidisciplinary integration of diverse fields: soft computing, machine learning, and the outranking approach. The brilliant contributions of Greco et al. (1997, 1999, 2001, 2002a, 2002b, 2005), Slowinski et al. (2005), and Szelag et al. (2013) on this emerging field have inspired us to propose new hybrid MCDM models to resolve practical problems, especially regarding improvement planning. The proposed framework of the new hybrid MCDM models is discussed in Subsection 2.3.
1.7 Outline of the Book Aside from this background of MCDM research and certain computational intelligence techniques for problem solving, the remainder of this book comprises two parts; the first part introduces the essential concepts and theories of relevant methods and techniques, and certain real-world applications, mainly in financial and IT industries, are illustrated in the second part. Although the cases discussed in this book mainly fall in the category of business, the proposed hybrid approach for problem solving is not limited to this field; numerous types of real-world problems, in fields like economics, business, psychology, social welfare, engineering, transportation planning, new product development, and national policy formation, can be addressed using these methods. In addition, the three pillars—MRDM, MADM, and MODM—may be regarded as three types of methods for solving different types of problems, and the combination or integration of the techniques from those three fields should be based on the problems that are addressed. The details of the new hybrid approach are discussed in the following chapters. We hope that interested readers may find it helpful to apply the new hybrid MCDM models for solving real-world problems in various fields, thus bridging the gap between academia and practice. CHAPTER TWO
NEW CONCEPTS AND TRENDS IN MCDM |
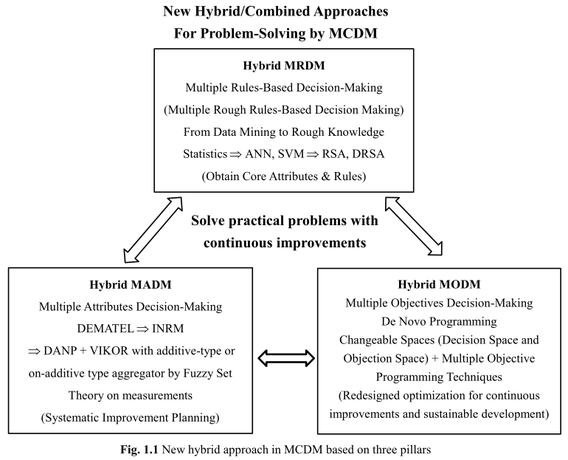
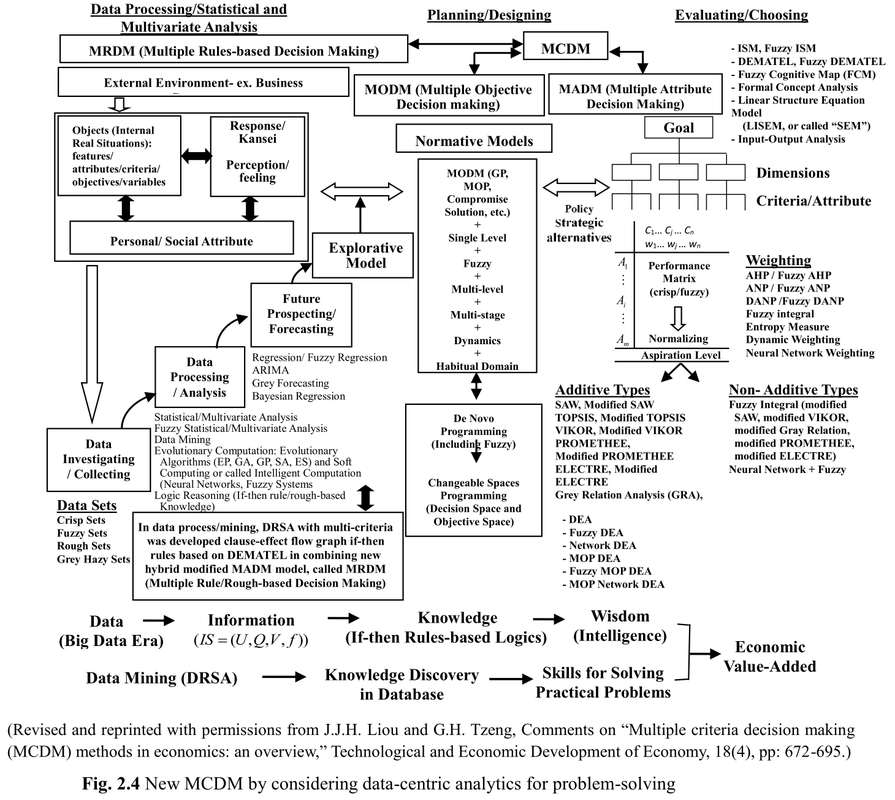
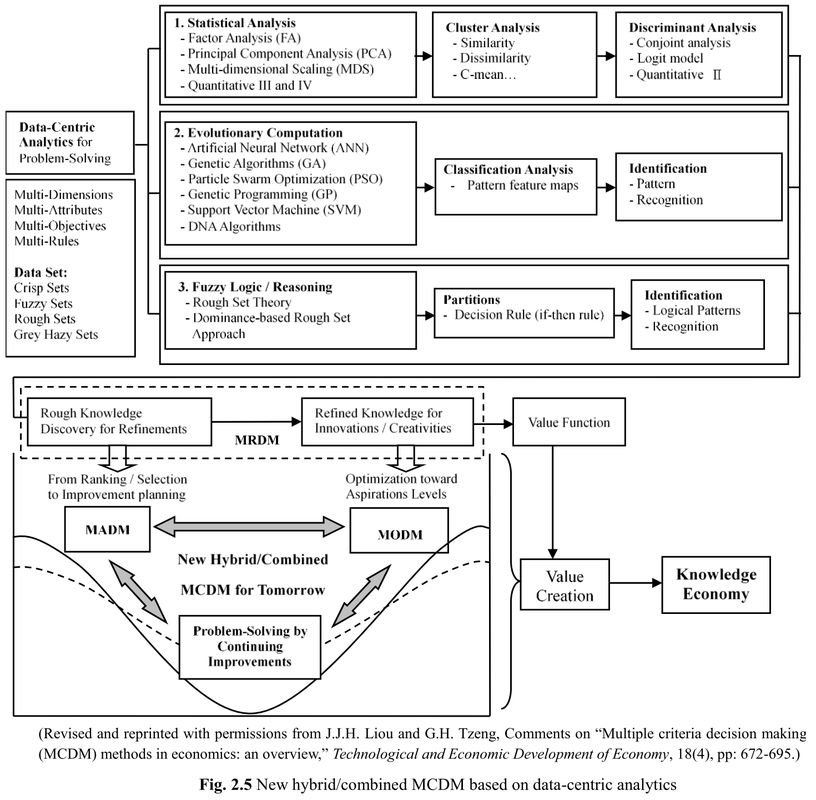
Before delving into detailed discussions of solving problems with MCDM, this chapter provides an overview of the three building blocks of the new hybrid MCDM approach, as proposed in recent years by Prof. Tzeng’s research group. As shown in Fig. 1.1, the three subfields in this new MCDM are (1) hybrid MRDM, (2) hybrid MADM, and (3) hybrid MODM.
Although the algorithms related to hybrid MRDM might be complicated, the essential ideas are easy to comprehend; two new concepts from MRDM are as follows:
a. Critical factors or criteria can be objectively retrieved from historical data
The growing complexity in social problems has impeded identification of the most crucial variables for modeling by intuition or conventional linear methods (e.g., statistics). MRDM leverages the strengths of computational intelligence by retrieving the critical factors for forming hybrid decision models, which are more reasonable and reliable in practice.
b. MRDM can induct understandable decision rules in the form of “if…, then…” logics
The manifest benefit of understandable decision rules is that they are close to how human brains learn from experience or examples.
Usually in hybrid MADM, two or more analytical MADM methods (techniques) are combined or integrated for ranking, selection, and improvement planning, in the context of multiple attributes. Four new concepts are highlighted here:
a. Nearly all the considered attributes in a MADM problem are interrelated
Traditional methods, such as regression and analytic hierarchy process (AHP), must presume that all attributes are independent; this assumption sometimes works in certain engineering applications; however, analysts of most social problems, ranging from business to national policy-making, must concede that interrelations do exist between variables in most cases. Adequate methods that can acknowledge and measure those interrelations are required in practice.
b. Pursuing aspiration levels Traditional
MADM methods often define a goal for each attribute; that goal is often derived from comparisons of a group of readily available alternatives. This might lead decision makers (DMs) to be satisfied with the available solutions. A new concept in MADM is that DMs can pursue aspiration levels to avoid stagnation at the local optima. The importance of this concept is magnified in highly competitive business environments. Consider a country in which the service quality of each airline is rated on a scale of 0–100 points. If only five domestic airlines operated in this country and their service quality scores ranged from 60 to 78, it would be problematic to adopt the highest one (because 78 is far from excellent) as the benchmark or goal; the management teams of those operators should set the full score as their aspiration level and plan for continuous improvements; otherwise, those domestic operators would find it difficult to survive under the pressure of global competition.
c. Systematic improvements for the underperformed attributes
Once the underperforming attributes are identified, systematic improvement planning is required. As the aforementioned interrelations among attributes do exist in most social problems, a plan for systematic improvement should identify the source factors that influence those underperforming attributes. Using medical treatment as an analogy: if a patient is suffering from a headache caused by work-related stress and high blood pressure (hypertension), it would be in vain to treat the patient by merely administering aspirin to him. The concept of systematic improvements is explained using several empirical cases in the second part of this book.
d. Nonadditive performance aggregation
The influences of this new concept are twofold. First, when modeling the preference (which economists call “utility”) of a DM, nonadditive effects are not rare. When consumers evaluate smartphones, for example, although several factors (e.g., function, price, quality, and so on) are considered simultaneously, consumers might be overwhelmingly influenced by appealing designs that are easy to use, which partially explains the leading position of the iPhone. Second, certain complicated social or business phenomena have the so-called “synergy effect” (1 + 1≠2), which is commonly observed in strategic alliances or merger and acquisition deals. A case of vendor selection is illustrated in Chapter 14 by using nonadditive performance aggregation.
Finally, in hybrid MODM, a new concept called “changeable spaces” is introduced. Conventional MODM research is confined by the assumption of fixed resources; DMs thus tend to accede to compromised solutions. The concept of “changeable spaces” attempts to challenge the existing frameworks or constraints by offering a new perspective on redesigning or redefining a system. The details are discussed in Chapter 6 with illustrations. As stated in Subsection 1.2, compared with the statistical approach, MCDM research puts more emphasis on problem solving. In this chapter, the basic concepts of problem solving and certain topics that are often ignored in traditional MCDM research are discussed; in addition, a new framework of hybrid MCDM is proposed to address those underexplored topics.
2.1 Problem Solving in Traditional MCDM
Traditional MCDM research often begin with a predefined problem: single or multiple goals, multiple criteria (in MADM), or multiple constraints (in MODM). Limited alternatives can then be ranked or selected (in MADM), or an efficient frontier can be obtained for the optimal resource allocation (in MODM). However, two underexplored but critical issues must be addressed in traditional MCDM research: (1) the initial problem definition might exert unexpected influence on the obtained results, and (2) decision-making should play a more constructive role in problem solving. Merely ranking solutions or optimizing based on existing constraints might not suffice to determine an optimal solution. The two critical issues are discussed in the followings. For the first point, the involved or observed criteria (or attributes) in MCDM research are usually obtained from three approaches: (1) subjective judgments by researchers; (2) statistical analysis from historical data; and (3) theoretical support. The subjective judgment approach is constrained by the limited knowledge and experience of researchers; in addition, real-world problems are becoming ever more complex and complicated; it would be unlikely for researchers to choose the minimal and essential criteria (attributes) when considering numerous plausible attributes (e.g., 25 or more) by subjective judgments. This could be explained by bounded rationality, a concept proposed by Nobel Prize laureate H.A. Simon (1972, 1982) in the context of economics. The statistical approach has certain unrealistic assumptions such as the independence of the considered variables and questionable probabilistic assumptions regarding data, which are discussed in Subsection 1.2. Theoretical support seems to be ideal at first glance, but a real-world problem is often based on (or rooted in) a specific context. Generalized theories might not suffice for a specific case; therefore, merely using theories to select the minimal and critical criteria (variables) might not be practical for a real case.
Second, MCDM research should play a more proactive or constructive role in problem solving; to select among a group of inferior options would not help DMs achieve satisfactory outcomes. For example, once a performance evaluation model has been constructed by certain MADM methods, such as AHP or ANP, researchers or practitioners (e.g., the management team of a company) may consider how to improve the proposed alternative. Most previous MCDM research has ignored the idea of improvement planning on problem solving. Traditional MODM studies only make plans regarding their predefined constraints and resources; but in a dynamic and rapidly changing environment, DMs must pursue methods to extend the currently known area of competence to achieve their aspiration levels.
To summarize, traditional MCDM research has ignored the aforementioned two essential questions/issues for problem solving, and the specific reasons for adopting the new hybrid MCDM approach are discussed in Subsection 2.2.
2.2 Why New Hybrid MCDM Approaches Are Needed
As mentioned in Subsections 1.1 and 2.1, DMs might find that traditional MCDM techniques are not sufficient to resolve complicated and entwined problems in practice; therefore, we highlight the background and specific motivations of the new concepts and trends in MCDM as follows.
First, as discussed in Subsection 2.1, traditional MCDM studies have ignored the objective and reliable selection of minimal and representative criteria for forming MCDM models. Complex social or business environments require reasonable approaches to help researchers identify critical attributes. In the so-called “Big Data era,” human brains (i.e., of DMs or researchers) inevitably encounter difficulties when they attempt to process the complex and imprecise patterns behind a complex problem (or information system).
Second, most traditional MADM studies have either focused on obtaining final ranking results or forming a utility function to aid DMs; however, traditional MADM studies have typically overlooked the relationships among the involved criteria and have failed to identify the imprecise reasoning embedded in their criteria with respect to the addressed problem.
Third, traditional MCDM models assume that the criteria are independent and hierarchical in structure; however, in most real-world problems, the relationships among criteria or aspects (also called dimensions) are usually interdependent with certain feedback effects. To identify the interrelated relationships among variables, the DEMATEL technique can build influential network relations map (INRM) and find the influential weights of DANP by using the basic concept of ANP (Saaty 1996), based on the influential relationship matrix of DEMATEL (Ou Yang et al. 2008, 2013; Peng and Tzeng 2013; Shen et al. 2014; Hu et al. 2014). This can model some interdependent and feedback relationships among criteria. It also helps DMs avoid unrealistic assumptions of statistics and economics when resolving practical problems.
Fourth, the proposed method replaces the relatively favorable solutions of existing alternatives with aspiration levels that can support DMs in pursuit of excellence. Aspiration levels were proposed by H.A. Simon (1955, 1956, and 1959) as replacements for classical selections or optimization decisions based on min–max values. By searching for aspiration levels at each stage, the decision process can become a pursuit for continuous improvements or enhancements. Therefore, the classical VIKOR method was modified (Opricovic and Tzeng 2004, 2007) by correcting the traditional settings that adopt max–min values as ideal and negative ideal points. In the modified VIKOR, the aspiration level and the least desirable values on each criterion are used instead to avoid decisions that “pick the best apple in a barrel of rotten apples.”
Fifth, the new hybrid MADM analytical tools are not only used for ranking or selection; they can also be used to improve performance gaps for multiple criteria and the corresponding aspects (or dimensions). Therefore, the emphasis in the research field has shifted from ranking or selection when determining the most preferable approaches to performance improvement of existing methods according to INRM, because a systematic approach for problem solving is required. Instead of addressing the systems of the problem, the sources of the problem must be identified for performance improvement (i.e., improvement planning) to avoid stop-gap piecemeal measures.
Sixth, Kahneman (who received the Nobel Prize in Economics in 2002) and Tversky used an additive-type utility aggregation model based on their works during the 1960s and found that consumers’ product selection behaviors were not in accordance with the traditional concept of multiattribute utility. The traditional notion of multiattribute utility is value-function aggregation. They opined that traditional multiattribute utility models might not indicate consumers’ real behaviors. In 1974, Sugeno completed his doctoral thesis, “Theory of fuzzy integrals and its applications,” at the Tokyo Institute of Technology. In that work, fuzzy integrals were proposed to aggregate the values of multiple attributes in a nonadditive approach. The mathematical modeling of nonadditive aggregation (i.e., value functions) could correct the problematic assumption—linear independence—found in traditional additive-type models. This fact inspired Kahneman to propose prospect theory in 1978 by adopting the basic concept from nonadditive aggregation.
Seventh, conventional MODM methods in planning and design are based on a decision space defined by a set of fixed conditions or resources. The objective function is defined in a feasible space of fixed requirements. (The fixed feasible region is called the “objective space.”) New concepts, especially MODM models with changeable spaces, may transform or extend those fixed requirements or constraints, facilitating searches for results approaching aspiration levels. This new thinking in changeable spaces programming can help DMs achieve win–win planning and design, and also can identify the desired points (aspiration levels) for continuous improvements. Therefore, these new concepts are expected to be superior to searches for Pareto optimal solutions or ideal points; the concept of changeable spaces is shown in Fig. 2.1. The details are explained and discussed in Chapter 6. The aforementioned seven points echo the new concepts highlighted at the beginning of this chapter.
Although the algorithms related to hybrid MRDM might be complicated, the essential ideas are easy to comprehend; two new concepts from MRDM are as follows:
a. Critical factors or criteria can be objectively retrieved from historical data
The growing complexity in social problems has impeded identification of the most crucial variables for modeling by intuition or conventional linear methods (e.g., statistics). MRDM leverages the strengths of computational intelligence by retrieving the critical factors for forming hybrid decision models, which are more reasonable and reliable in practice.
b. MRDM can induct understandable decision rules in the form of “if…, then…” logics
The manifest benefit of understandable decision rules is that they are close to how human brains learn from experience or examples.
Usually in hybrid MADM, two or more analytical MADM methods (techniques) are combined or integrated for ranking, selection, and improvement planning, in the context of multiple attributes. Four new concepts are highlighted here:
a. Nearly all the considered attributes in a MADM problem are interrelated
Traditional methods, such as regression and analytic hierarchy process (AHP), must presume that all attributes are independent; this assumption sometimes works in certain engineering applications; however, analysts of most social problems, ranging from business to national policy-making, must concede that interrelations do exist between variables in most cases. Adequate methods that can acknowledge and measure those interrelations are required in practice.
b. Pursuing aspiration levels Traditional
MADM methods often define a goal for each attribute; that goal is often derived from comparisons of a group of readily available alternatives. This might lead decision makers (DMs) to be satisfied with the available solutions. A new concept in MADM is that DMs can pursue aspiration levels to avoid stagnation at the local optima. The importance of this concept is magnified in highly competitive business environments. Consider a country in which the service quality of each airline is rated on a scale of 0–100 points. If only five domestic airlines operated in this country and their service quality scores ranged from 60 to 78, it would be problematic to adopt the highest one (because 78 is far from excellent) as the benchmark or goal; the management teams of those operators should set the full score as their aspiration level and plan for continuous improvements; otherwise, those domestic operators would find it difficult to survive under the pressure of global competition.
c. Systematic improvements for the underperformed attributes
Once the underperforming attributes are identified, systematic improvement planning is required. As the aforementioned interrelations among attributes do exist in most social problems, a plan for systematic improvement should identify the source factors that influence those underperforming attributes. Using medical treatment as an analogy: if a patient is suffering from a headache caused by work-related stress and high blood pressure (hypertension), it would be in vain to treat the patient by merely administering aspirin to him. The concept of systematic improvements is explained using several empirical cases in the second part of this book.
d. Nonadditive performance aggregation
The influences of this new concept are twofold. First, when modeling the preference (which economists call “utility”) of a DM, nonadditive effects are not rare. When consumers evaluate smartphones, for example, although several factors (e.g., function, price, quality, and so on) are considered simultaneously, consumers might be overwhelmingly influenced by appealing designs that are easy to use, which partially explains the leading position of the iPhone. Second, certain complicated social or business phenomena have the so-called “synergy effect” (1 + 1≠2), which is commonly observed in strategic alliances or merger and acquisition deals. A case of vendor selection is illustrated in Chapter 14 by using nonadditive performance aggregation.
Finally, in hybrid MODM, a new concept called “changeable spaces” is introduced. Conventional MODM research is confined by the assumption of fixed resources; DMs thus tend to accede to compromised solutions. The concept of “changeable spaces” attempts to challenge the existing frameworks or constraints by offering a new perspective on redesigning or redefining a system. The details are discussed in Chapter 6 with illustrations. As stated in Subsection 1.2, compared with the statistical approach, MCDM research puts more emphasis on problem solving. In this chapter, the basic concepts of problem solving and certain topics that are often ignored in traditional MCDM research are discussed; in addition, a new framework of hybrid MCDM is proposed to address those underexplored topics.
2.1 Problem Solving in Traditional MCDM
Traditional MCDM research often begin with a predefined problem: single or multiple goals, multiple criteria (in MADM), or multiple constraints (in MODM). Limited alternatives can then be ranked or selected (in MADM), or an efficient frontier can be obtained for the optimal resource allocation (in MODM). However, two underexplored but critical issues must be addressed in traditional MCDM research: (1) the initial problem definition might exert unexpected influence on the obtained results, and (2) decision-making should play a more constructive role in problem solving. Merely ranking solutions or optimizing based on existing constraints might not suffice to determine an optimal solution. The two critical issues are discussed in the followings. For the first point, the involved or observed criteria (or attributes) in MCDM research are usually obtained from three approaches: (1) subjective judgments by researchers; (2) statistical analysis from historical data; and (3) theoretical support. The subjective judgment approach is constrained by the limited knowledge and experience of researchers; in addition, real-world problems are becoming ever more complex and complicated; it would be unlikely for researchers to choose the minimal and essential criteria (attributes) when considering numerous plausible attributes (e.g., 25 or more) by subjective judgments. This could be explained by bounded rationality, a concept proposed by Nobel Prize laureate H.A. Simon (1972, 1982) in the context of economics. The statistical approach has certain unrealistic assumptions such as the independence of the considered variables and questionable probabilistic assumptions regarding data, which are discussed in Subsection 1.2. Theoretical support seems to be ideal at first glance, but a real-world problem is often based on (or rooted in) a specific context. Generalized theories might not suffice for a specific case; therefore, merely using theories to select the minimal and critical criteria (variables) might not be practical for a real case.
Second, MCDM research should play a more proactive or constructive role in problem solving; to select among a group of inferior options would not help DMs achieve satisfactory outcomes. For example, once a performance evaluation model has been constructed by certain MADM methods, such as AHP or ANP, researchers or practitioners (e.g., the management team of a company) may consider how to improve the proposed alternative. Most previous MCDM research has ignored the idea of improvement planning on problem solving. Traditional MODM studies only make plans regarding their predefined constraints and resources; but in a dynamic and rapidly changing environment, DMs must pursue methods to extend the currently known area of competence to achieve their aspiration levels.
To summarize, traditional MCDM research has ignored the aforementioned two essential questions/issues for problem solving, and the specific reasons for adopting the new hybrid MCDM approach are discussed in Subsection 2.2.
2.2 Why New Hybrid MCDM Approaches Are Needed
As mentioned in Subsections 1.1 and 2.1, DMs might find that traditional MCDM techniques are not sufficient to resolve complicated and entwined problems in practice; therefore, we highlight the background and specific motivations of the new concepts and trends in MCDM as follows.
First, as discussed in Subsection 2.1, traditional MCDM studies have ignored the objective and reliable selection of minimal and representative criteria for forming MCDM models. Complex social or business environments require reasonable approaches to help researchers identify critical attributes. In the so-called “Big Data era,” human brains (i.e., of DMs or researchers) inevitably encounter difficulties when they attempt to process the complex and imprecise patterns behind a complex problem (or information system).
Second, most traditional MADM studies have either focused on obtaining final ranking results or forming a utility function to aid DMs; however, traditional MADM studies have typically overlooked the relationships among the involved criteria and have failed to identify the imprecise reasoning embedded in their criteria with respect to the addressed problem.
Third, traditional MCDM models assume that the criteria are independent and hierarchical in structure; however, in most real-world problems, the relationships among criteria or aspects (also called dimensions) are usually interdependent with certain feedback effects. To identify the interrelated relationships among variables, the DEMATEL technique can build influential network relations map (INRM) and find the influential weights of DANP by using the basic concept of ANP (Saaty 1996), based on the influential relationship matrix of DEMATEL (Ou Yang et al. 2008, 2013; Peng and Tzeng 2013; Shen et al. 2014; Hu et al. 2014). This can model some interdependent and feedback relationships among criteria. It also helps DMs avoid unrealistic assumptions of statistics and economics when resolving practical problems.
Fourth, the proposed method replaces the relatively favorable solutions of existing alternatives with aspiration levels that can support DMs in pursuit of excellence. Aspiration levels were proposed by H.A. Simon (1955, 1956, and 1959) as replacements for classical selections or optimization decisions based on min–max values. By searching for aspiration levels at each stage, the decision process can become a pursuit for continuous improvements or enhancements. Therefore, the classical VIKOR method was modified (Opricovic and Tzeng 2004, 2007) by correcting the traditional settings that adopt max–min values as ideal and negative ideal points. In the modified VIKOR, the aspiration level and the least desirable values on each criterion are used instead to avoid decisions that “pick the best apple in a barrel of rotten apples.”
Fifth, the new hybrid MADM analytical tools are not only used for ranking or selection; they can also be used to improve performance gaps for multiple criteria and the corresponding aspects (or dimensions). Therefore, the emphasis in the research field has shifted from ranking or selection when determining the most preferable approaches to performance improvement of existing methods according to INRM, because a systematic approach for problem solving is required. Instead of addressing the systems of the problem, the sources of the problem must be identified for performance improvement (i.e., improvement planning) to avoid stop-gap piecemeal measures.
Sixth, Kahneman (who received the Nobel Prize in Economics in 2002) and Tversky used an additive-type utility aggregation model based on their works during the 1960s and found that consumers’ product selection behaviors were not in accordance with the traditional concept of multiattribute utility. The traditional notion of multiattribute utility is value-function aggregation. They opined that traditional multiattribute utility models might not indicate consumers’ real behaviors. In 1974, Sugeno completed his doctoral thesis, “Theory of fuzzy integrals and its applications,” at the Tokyo Institute of Technology. In that work, fuzzy integrals were proposed to aggregate the values of multiple attributes in a nonadditive approach. The mathematical modeling of nonadditive aggregation (i.e., value functions) could correct the problematic assumption—linear independence—found in traditional additive-type models. This fact inspired Kahneman to propose prospect theory in 1978 by adopting the basic concept from nonadditive aggregation.
Seventh, conventional MODM methods in planning and design are based on a decision space defined by a set of fixed conditions or resources. The objective function is defined in a feasible space of fixed requirements. (The fixed feasible region is called the “objective space.”) New concepts, especially MODM models with changeable spaces, may transform or extend those fixed requirements or constraints, facilitating searches for results approaching aspiration levels. This new thinking in changeable spaces programming can help DMs achieve win–win planning and design, and also can identify the desired points (aspiration levels) for continuous improvements. Therefore, these new concepts are expected to be superior to searches for Pareto optimal solutions or ideal points; the concept of changeable spaces is shown in Fig. 2.1. The details are explained and discussed in Chapter 6. The aforementioned seven points echo the new concepts highlighted at the beginning of this chapter.
2.3 Framework of the New Hybrid MCDM Models for Tomorrow
On the basis on the aforementioned two issues of traditional MCDM in Subsection 2.1 and the seven specific motivations in Subsection 2.2, a framework of the new hybrid MCDM models for problem solving is proposed herein. The overall vision and main ideas are illustrated in Fig. 2.2. Two key points of the proposed conceptual framework are further illustrated in Fig. 2.3: (1) Identify the core criteria and rough knowledge in a complex environment for appropriate problem settings, and (2) explore the interrelated cause–effect relationships among the core criteria and rough knowledge (e.g., rules, logic, and fuzzy inferences) for systematic improvement planning.
On the basis on the aforementioned two issues of traditional MCDM in Subsection 2.1 and the seven specific motivations in Subsection 2.2, a framework of the new hybrid MCDM models for problem solving is proposed herein. The overall vision and main ideas are illustrated in Fig. 2.2. Two key points of the proposed conceptual framework are further illustrated in Fig. 2.3: (1) Identify the core criteria and rough knowledge in a complex environment for appropriate problem settings, and (2) explore the interrelated cause–effect relationships among the core criteria and rough knowledge (e.g., rules, logic, and fuzzy inferences) for systematic improvement planning.
Fig. 2.2 Main ideas of problem-solving in new hybrid MCDM
Fig. 2.3 Conceptual framework of new hybrid/combined MCDM
Traditional MCDM research has not adequately addressed the complexity of data, but rapidly growing, information-centric research on practical contemporary problems cannot overlook such complexity. As a result, in this book, we expand past notions of MADM and MODM by further incorporating the field of data-centric analytics, such as statistical analyses, machine learning, soft computing, and data mining techniques (as shown on the left side of Fig. 2.4).
Data-centric analytics can be further simplified into multiple rules-based decision-making (i.e., MRDM, as shown in Fig. 1.1), which is aimed at retrieving critical attributes or criteria to form hybrid MADM or MODM models with understandable rules or logic. The details of data-centric analytics are further illustrated in Fig. 2.5.
Therefore, the modeling of new hybrid MCDM may be regarded as a process of transforming data (or information) and knowledge (or experience) from experts (or DMs) to form understandable decision aids for problem solving. This new framework is proposed to leverage the strengths of the computational capabilities of machines and the knowledge and experience of human beings for enhancing the problem solving capability in various fields. Such enhancements can foster the growth of the future knowledge economy. The new concepts, theoretical backgrounds, and applications introduced in the following chapters are summarized in Table 2.1. It is not necessary to read those chapters in sequence; readers who are interested in a specific subfield (i.e., hybrid MRDM, hybrid MADM, or MODM) may find it useful to examine the associated empirical application(s) after reading the theoretical chapter(s).
Table 2.1 Overview of the following chapters
|
Multiple Attribute Decision Making: Methods and Application
By Gwo-Hshiung Tzeng & Jih-Jeng Huang (2011), CRC Press, Taylor & Francis Group, A Chapman & Hall Book.
Part I Concepts and Theory of MADM
Analytic Hierarchy Process; Analytic Network Process and Fuzzy Analytic Network Process; Simple Additive Weighting Method; TOPSIS and VIKOR; ELECTRE Method; PROMETHEE Method; Gray Relational Model; Fuzzy Integral Technique; Rough Sets; Structural Model (Interpretive Structural Modeling (ISM) Method, DEMATEL Method, Fuzzy Cognition Maps). Part II Applications of MADM AHP: An Application; VIKOR Technique with Applications Based on DEMATEL and ANP; TOPSIS and VIKOR: An Application; ELECTRE: An Application; PROMETHEE: An Application; Fuzzy Integral and Gray Relation: An Application; Fuzzy Integral: An Application; Rough Sets: An Application. |
Fuzzy Multiple Objective Decision Making
By Gwo-Hshiung Tzeng & Jih-Jeng Huang (2013), CRC Press, Taylor & Francis Group, A Chapman & Hall Book.
Section
I Concepts and Theory of Multi-Objective Decision Making
Multi-Objective Evolutionary Algorithms; Goal Programming; Compromise Solution and TOPSIS; De Novo Programming and Changeable Parameters (including Decision Space and Objective Space, called Changeable Spaces); Multi-Stage Programming; Multi-Level Multi-Objective Programming; Data Envelopment Analysis. Section II Applications of Multi-Objective Decision Making Motivation and Resource Allocation for Strategic Alliances; Choosing Best Alliance Partners and Allocating Optimal Alliance Resources Using Fuzzy Multi-Objective Dummy Programming Model; Multi-Objective Planning for Supply Chain Production and Distribution Mode: Bicycle Manufacturer; Fuzzy interdependent Multi-Objective Programming; Novel Algorithm for Uncertain Portfolio Selection; Multi-objective Optimal Planning for Designing Relief Delivery Systems; Comparative Productivity Efficiency for Global Telecoms; Fuzzy Multiple Objective Programming in Interval Piecewise Regression Model. |
|
New MCDM Books (MADM & MODM)
Gwo-Hshiung Tzeng Gwo-Hshiung Tzeng, Jih-Jeng Huang (2012). Multiple Attribute Decision Making: Methods and Applications, CRC Press, Taylor & Francis Group, 2011, 349 pages. Gwo-Hshiung Tzeng, Jih-Jeng Huang (2013). Fuzzy Multiple Objective Decision Making, CRC Press, Taylor & Francis Group, 2013, 313 pages Gwo-Hshiung Tzeng, Kao-Yi Shen (2016). New Concepts and Trends of Hybrid Multiple Criteria Decision Making, CRC Press, Taylor & Francis Group, In Press. Tzeng, G.H.; Kao-Yi Shen, K.Y. New Concepts and Trends of Hybrid Multiple Criteria Decision Making, CRC Press, Taylor & Francis Group, 2016, In Press. New Concepts and Trends of Hybrid Multiple Criteria Decision Making including three parts: (1) Hybrid MRDM (Multiple Rule/Rough-based Decision Making), (2) Hybrid MADM (Multiple Attribute Decision Making, (3) Hybrid MODM (Multiple Objective Decision Making). The features and contributions of this new book are shown as followings: In Hybrid MRDM (Multiple Rule/Rough-based Decision Making), First, for avoiding "Statistics and Economics are unrealistic in assumptions/ hypotheses: How can be easy to understand and control from “Big-Data” to extract the “CORE Attribute” for decision-makers in making decision through/combining MADM and MODM; Tzeng’s research group using logical thinking and reasoning based on basic concept of “Rough Set Theory (RST)” to construct the core attributes in if-then rules” from “Big Data”. Furthermore, this book uses the “DRSA (dominance-based rough set approach) or VC-DRSA” to build “Flow Graph” in “if-then rule-based” combining DEMATEL technique to construct the cause-effect in “if-then Rule/Rough-based Decision-Making” (called Multiple Rule/Rough-based Decision Making, MRDM) as influential relationship flow, called MRDM. These results can make decision-makers or users easy to understand and grasp the problems in the causal-effect relationship combining DEMATEL technique. So we also can combine the "new hybrid MCDM model”, can more obtain effectively to provide the decision-makers for solving the real world problems-improving. In Hybrid MADM (Multiple Attribute Decision Making), Second-Fifth items), Second, how can find the influence relation matrix in the key "aspects and criteria" to establish the Influential Network Relation Map (INRM) and find the influential weights of DANP (DEMATEL-based ANP) in dependence and feedback problems by cause-effect via interrelationship in the practical situations;”?. The traditional model assumes the criteria are independent and hierarchical in structure; the previous studies that mainly rely on statistical models (e.g., regressions and time series models) to examine the relationship based on independence, linear, correlation, etc. However, in real-world problems, the interrelationships between the criteria or aspects (or called dimensions) are usually interdependent and sometimes even exert feedback effects; So we adopt DEMATEL method to construct influential network relation map (INRM) and to find the influential weights of DANP using basic concept of ANP (Saaty, 1996) based on influence relation matrix of DEMATEL technique (Ou Yang et al., 2008, 2013; Peng and Tzeng, 2013; Shen et al., 2014; Hu et al., 2014) for solving the inter-dependence and feedback (interrelationship problems) of criteria (or called attributes) aspects (or called dimensions) in the real world problem to avoid “unrealistic assumptions in Statistics and Economics”. Third, how fulfill “problem-solving and improvement (Adopting “aspired-worst” to replace traditional “max-min” as benchmark)” for the overall consideration “aspects and criteria” can be all towards for reaching “aspiration level”? The relative good solution from the existing alternatives is replaced by the aspiration levels to fit today’s competitive markets; so we modified VIKOR method (Opricovic and Tzeng, 2004, 2007), SAW, Grey Relation Analysis (Chiu et al., 2014, Liou et al., 2015), PROMETHEE (Tsui et sl., 2015), ELECTRE to correct traditional Max-Min as ideal point and negative ideal point into aspiration level and the worst value. The relatively good solution from existing alternatives based on “max-min” as goal/target (benchmark) is replaced by aspiration level and worst value (“aspired-worst” as benchmark) for avoiding “Choosing the best among inferior options/alternatives”, i.e. for avoiding “pick the best apple among a barrel of rotten apples”. Simon incorporated the basic concept of the “aspiration level” in his work, receiving the Nobel Prize in Economics in 1978. HA Simon - Decision and organization, 1972 - innovbfa.viabloga.com ... The Scottish word "satisficing" (=satisfying) has been revived to denote problem solving and decision making that sets an aspiration level, searches until an alternative is found that is satisfactory by the aspiration level criterion, and selects that alternative (Simon (1957), Part IV ... (Simon, 1978, Nobel Prize). For example, the performance value of each criterion can be obtained by using questionnaires with a scale ranging from 0 points (complete dissatisfaction/bad) to 10 points (the best satisfaction/good). Then in this case, we can set the aspiration level as ten (10) and the worst value as zero (0) j=1,2,…,n, called “aspired-worst” as benchmark. In contrast to the traditional approach, which sets the best and the worst value in each criterion j as maximal and minimal performance for all alternatives k=1,2,…K respectively, called “max-min” as benchmark. Fourth, how can build the integrity (overall-view) of improvement strategies by systematics based on INRM? The new hybrid MADM analytical tools are not only used in ranking and selection, but also can be used in the performance gaps improvement among criteria and its corresponding aspects (or dimensions); So the emphasis in the field has shifted from ranking and selection when determining the most preferable approaches to performance improvement of existing methods based on INRM, because "we need a systematic approach to problem-solving; instead of addressing the systems of the problem, i.e., we need to identify the sources of the problem in performance improvement based on INRM, because “we need a systematic approach to problem-solving; instead of addressing the systems of the problem, we, to avoid “stop-gap piecemeal”. Fifth, how can build the integrity (overall-view) of improvement strategies by systematics based on INRM? Kahneman and Tversky (Kahneman received the Nobel Prize in Economics in 2002), they, in results of many their studies during 1960s, found consumers in products-selecting of multi-attribute preference value are almost different from traditional multi-attribute utility (value-function aggregation in multi-attribute) by using additive model. , i.e., almost all the results are inconsistent with the real actual problems, when they mistakenly thought preference people have problems Until 1974, Sugeno completed his Doctoral thesis “Theory of fuzzy integrals and its applications” in Tokyo Institute of Technology; fuzzy integrals are, namely, “non-additive model” or so-called “super-additive model”, as a value-function integrated model. So Kahneman based on above basic concept proposed “Prospect Theory” in 1978. In Hybrid MODM (Multiple Objective Decision Making), Sixth, based on above points five we can be systematically how find overall thinking the problem-improving for achieving or toward “aspiration levels, the resolve of implementing improvement-strategies in enforcement, how can enforce it? Classical MODM (Multiple Objectives Decision Making) in thinking of plan/design is based on a fixed set conditions or resources (fixed conditions or resources, this is called “Decision Space”, in feasible space to be fixed (i.e., fixed feasible region, this is called “Objective Space”) how we can find the Pareto optimal solution? We will propose a new thinking of “MODM models with changeable spaces” to implement and enforce for improvement in solving MADM problems for enhancing the performance values toward achieving the aspiration levels in criteria, dimensions, and overall through innovation and creativity. This new thinking in changeable spaces programming not only can help decision-makers to reach win-win planning or design, but also can be forward achieving the desired point (aspiration level), which is better than pursuing the Pareto optimal solutions or ideal point. |
Liou, James J.H. and Tzeng,
G.H. (Corresponding author) (2012),
Comments on "Multiple criteria decision making (MCDM) methods in
economics: An overview", Technological and Economic Development of Economy, 18(4),
672-695.
Abstract. This paper offers comments on a previously published paper, titled “Multiple criteria decision making (MCDM) methods in economics: an overview,” by Zavadskas and Turskis (2011). The paper’s authors made great efforts to summarize MCDM methods but may have failed to consider several important new concepts and trends in the MCDM field for solving actual problems. First, the traditional model assumes the criteria are independently and hierarchically structured; however, in reality, problems are often characterized by interdependent criteria and dimensions and may even exhibit feedback-like effects. Second, relatively good solutions from the existing alternatives are replaced by aspiration levels to fit today’s competitive markets. Third, the emphasis in the field has shifted from ranking and selection when determining the most preferable approaches to performance improvement of existing methods. Fourth, information fusion techniques, including the fuzzy integral method, have been developed to aggregate the performances. Finally, the original fixed resources in multi-objective programming are divided such that both decision and objective spaces are changeable. In this paper, we add new concepts and provide comments that could be thought of as an attempt to complete the original paper.
Abstract. This paper offers comments on a previously published paper, titled “Multiple criteria decision making (MCDM) methods in economics: an overview,” by Zavadskas and Turskis (2011). The paper’s authors made great efforts to summarize MCDM methods but may have failed to consider several important new concepts and trends in the MCDM field for solving actual problems. First, the traditional model assumes the criteria are independently and hierarchically structured; however, in reality, problems are often characterized by interdependent criteria and dimensions and may even exhibit feedback-like effects. Second, relatively good solutions from the existing alternatives are replaced by aspiration levels to fit today’s competitive markets. Third, the emphasis in the field has shifted from ranking and selection when determining the most preferable approaches to performance improvement of existing methods. Fourth, information fusion techniques, including the fuzzy integral method, have been developed to aggregate the performances. Finally, the original fixed resources in multi-objective programming are divided such that both decision and objective spaces are changeable. In this paper, we add new concepts and provide comments that could be thought of as an attempt to complete the original paper.